
科目:初中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2007年广东省深圳市东湖中学九年级数学竞赛试卷(解析版) 题型:解答题
 ,同时求其差再除以
,同时求其差再除以 ,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008证明你的结论.
,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008证明你的结论.查看答案和解析>>
科目:初中数学 来源:2008年江苏省淮安市淮阴中学高中招生考试数学试卷(解析版) 题型:解答题
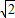 ,同时求其差再除以
,同时求其差再除以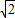 ,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008证明你的结论.
,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com