
 如图,锐角三角形ABC中,BC=6,BC边上的高线长为4,PQRS是△ABC的内接矩形,且S矩形PQRS=$\frac{1}{4}$S△ABC,记$\frac{BS}{BA}$=λ,求λ的值.
如图,锐角三角形ABC中,BC=6,BC边上的高线长为4,PQRS是△ABC的内接矩形,且S矩形PQRS=$\frac{1}{4}$S△ABC,记$\frac{BS}{BA}$=λ,求λ的值. 分析 可由△ASR∽△ABC得出对应边成比例,再由三角形与梯形的面积比建立等式,即可得出结论.
解答 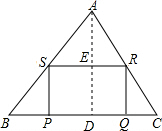 证明:如图,过A作AD⊥BC于D,交SR于E,
证明:如图,过A作AD⊥BC于D,交SR于E,
∵SR∥BC,
∴AE⊥SR,
设PS=x,RS=y,
∵SR∥BC,
∴△ASR∽△ABC,得$\frac{4-x}{4}=\frac{y}{6}$,
∴y=6-$\frac{3x}{2}$,
∵S矩形PQRS=$\frac{1}{4}$S△ABC,即x(6-$\frac{3x}{2}$)=$\frac{1}{4}×\frac{1}{2}$×6×4,
∴x=2+$\sqrt{2}$,或x=2-$\sqrt{2}$,
∴DE=PS=2+$\sqrt{2}$,或DE=PS=2-$\sqrt{2}$,
∵SR∥BC,∴$\frac{BS}{BA}$=$\frac{DE}{AD}$=λ,
∴λ=$\frac{2+\sqrt{2}}{4}$或λ$\frac{2-\sqrt{2}}{4}$.
点评 本题主要考查了相似三角形的判定及性质以及一元二次方程的求解问题,能够熟练掌握.


科目:初中数学 来源: 题型:解答题
 如图,△ABC中,D是BC的中点,AC∥BG,直线FG过点D交AC于F,交BG于G点,DE⊥GF,交AB于点E,连结GE、EF.
如图,△ABC中,D是BC的中点,AC∥BG,直线FG过点D交AC于F,交BG于G点,DE⊥GF,交AB于点E,连结GE、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在Rt△ABC中,AC=BC,∠ACB=90°,D是AC的中点,DG⊥AC交AB于点G.E为线段DC上任意一点,点F在线段DG上,且DE=DF,连结EF与CF,过点F作FH⊥FC,交直线AB于点H
在Rt△ABC中,AC=BC,∠ACB=90°,D是AC的中点,DG⊥AC交AB于点G.E为线段DC上任意一点,点F在线段DG上,且DE=DF,连结EF与CF,过点F作FH⊥FC,交直线AB于点H查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB和CD的端点A、B、C、D均在格点上.
图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB和CD的端点A、B、C、D均在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com