
【题目】如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )

A. 逐渐增加 B. 逐渐减小
C. 保持不变且与EF的长度相等 D. 保持不变且与AB的长度相等
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB﹣BD做匀速运动,动点Q从点D同时出发,沿着线路DC﹣CB﹣BA做匀速运动.

(1)求BD的长;
(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s.经过12秒后,P、Q分别到达M、N两点,试判断△AMN的形状,并说明理由,同时求出△AMN的面积;
(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为a cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
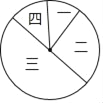
【题目】如图,一、二、三、四这四个扇形的面积之比为1:3:5:1.
(1)请分别求出它们圆心角的度数.
(2)一、二、四这三个扇形的圆心角的度数之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠ACB=90°,点E为△ABC内一点,且∠BEC=90°,将△BEC绕C点顺时针旋转90°,使BC与AC重合,得到△AFC,连接EF交AC于点M,已知BC=10,CF=6,则AM:MC的值为( ) 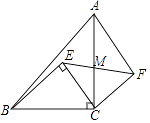
A.4:3
B.3:4
C.5:3
D.3:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树形图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上两点A,B对应的数分别是﹣1,3,点P为数轴上的一动点,其对应的数为x

(1)A、B两点的距离AB= ;
(2)在数轴上是否存在点P,使PA+PB=6?若存在,请求出x的值;若不存在,请说明理由.
(3)如图2,若点P以每秒1个单位的速度从点O出发向右运动,同时点A以每秒5个单位的速度向左运动,点B以每秒20个单位的速度向右运动,在运动的过程中,M、N分别是AP、OB的中点,问:![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com