
【题目】如图,已知抛物线y=![]() x+2与x轴交于A、B两点,交y轴于点C.
x+2与x轴交于A、B两点,交y轴于点C.

(1)判断△ABC的形状,并说明理由.
(2)在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)直角三角形,理由见解析;(2)存在,点P的坐标(﹣![]() ,0),(﹣
,0),(﹣![]() ,2+
,2+![]() ),(﹣
),(﹣![]() ,2﹣
,2﹣![]() ).
).
【解析】
(1)由二次函数图象上点的坐标特征求得点A、B、C的坐标,易得△ABC三边的长度,由勾股定理逆定理可以判定△ABC是直角三角形;
(2)该题中没有指出等腰三角形的底边,所用需要分类讨论:以AP为腰和以AP为底边两种情况,根据两点间的距离公式列出方程,通过解方程求得符合条件点P的坐标即可.
(1)直角三角形,理由如下:
当y=0时,﹣![]() x2﹣
x2﹣![]() x+2=0,解得,x1=﹣4,x2=1,
x+2=0,解得,x1=﹣4,x2=1,
即B(﹣4,0),A(1,0).
当x=0时,y=2,即C(0,2).
AB=1﹣(﹣4)=5,AB2=25,
AC2=(1﹣0)2+(0﹣2)2=5,
BC2=(﹣4﹣0)2+(0﹣2)2=20,
∵AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)存在,理由如下:
y=﹣![]() x2﹣
x2﹣![]() x+2的对称轴是x=﹣
x+2的对称轴是x=﹣![]() ,设P(﹣
,设P(﹣![]() ,n),
,n),
PA2=(1+![]() )2+n2=
)2+n2=![]() +n2,PC2=
+n2,PC2=![]() +(2﹣n)2,AC2=5.
+(2﹣n)2,AC2=5.
分类讨论:
①当AP=AC时,AP2=AC2,
![]() +n2=5,方程无解; 不存在.
+n2=5,方程无解; 不存在.
②当PA=PC时,PA2=PC2,
![]() +n2=
+n2=![]() +(2﹣n)2,
+(2﹣n)2,
解得,n=0,即P1(﹣![]() ,0);
,0);
③当CA=CP时CA2=CP2,![]() +(2﹣n)2=5,
+(2﹣n)2=5,
解得,n1=2+![]() ,n2=2﹣
,n2=2﹣![]() ,
,
故P2(﹣![]() ,2+
,2+![]() ),P3(﹣
),P3(﹣![]() ,2﹣
,2﹣![]() ).
).
综上所述:使得以A、C、P为顶点的三角形是等腰三角形,点P的坐标(﹣![]() ,0),(﹣
,0),(﹣![]() ,2+
,2+![]() ),(﹣
),(﹣![]() ,2﹣
,2﹣![]() ).
).


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠C=90°,AB=8![]() ,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
(1)当点G在AC边什么位置时,四边形CGOH是正方形.
(2)等腰直角三角ABC的边被Rt△DEF覆盖部分的两条线段CG与CH的长度之和是否会发生变化,如不发生变化,请求出CG与CH之和的值:如发生变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.

(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
(3)怎样围才能使围出的矩形场地面积最大?最大面积为多少?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )
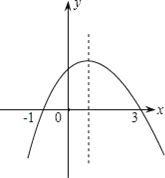
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )

A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级某班学生准备去购买《英汉词典》一书,此书的标价为20元.现A、B两书店都有此书出售,A店按如下方法促销:若只购买1本,则按标价销售;当一次性购买多于1本,但不多于20本时,每多购买一本,每本的售价在标价的基础上优惠2%(例如,买2本每本的售价优惠2%,买3本每本的售价优惠4%,依此类推);当购买多于20本时,每本的售价为12元.B书店一律按标价的7折销售.
(1)试分别写出在两书店购买此书的总价yA、yB与购书本数之间的函数关系式.
(2)若该班一次购买多于20本,去哪家书店购买更合算?为什么?若要一次性购买不多于20本,先写出y(y=yA﹣yB)与购书本数x之间的函数关系式,画出其函数图象,再利用函数图象分析去哪家书店购买更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面院墙,用篱笆围成一个外形为矩形的花圃,花圃的面积为S平方米,平行于院墙的一边长为x米.
(1)若院墙可利用最大长度为10米,篱笆长为24米,花圃中间用一道篱笆间隔成两个小矩形,求S与x之间的函数关系;
(2)在(1)的条件下,若围成的花圃面积为45平方米,求AB的长;
(3)在(1)的条件下,能否围成面积比45平方米更大的花圃?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+2x+3.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围;
③若经过点(0,k)且与x轴平行的直线l与y=-x2+2x+3的图像有公共点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com