练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．在Rt△ABC中，已知∠C=90°，a=17.5，c=62.5．解这个直角三角形．

    分析 由勾股定理求出b，再由三角函数求出∠A，即可得出∠B的度数．

    解答 解：∵∠C=90°，a=17.5，c=62.5．
    ∴b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{62．{5}^{2}-17．{5}^{2}}$=60，
    ∵sinA=$\frac{a}{c}$=$\frac{17.5}{62.5}$=0.28，
    ∴∠A≈16°，
    ∴∠B=90°-∠A=74°．

    点评 该题主要考查了解直角三角形、勾股定理、三角函数；熟练掌握勾股定理和三角函数的定义是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：[（ab+2）2-（1+2ab）（4-ab）]÷3ab，其中a=$\frac{3}{4}$，b=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：（$\sqrt{3}$+$\sqrt{2}$）-（$\sqrt{2}$-3$\sqrt{3}$）+|-2$\sqrt{3}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在Rt△ABD中，∠DAB=90°，AD=1，BD=$\sqrt{17}$，将△ABD沿着CE对折，使得点B与点D重合，折痕为CE．
    （1）求线段AB的长；
    （2）求线段BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，在?ABCD中，请添加一个条件：∠A=90°，使得?ABCD成为矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．当x≠3时，分式$\frac{1}{3-x}$有意义；
    当x=±2时，分式$\frac{x+1}{{x}^{2}-4}$无意义；
    当x=-3时，分式$\frac{3{x}^{2}-27}{x-3}$的值为0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．下表是抽取某校八年级（1）班20名学生一次数学测试的成绩统计表：
    成绩（分）60708090100
    人数（人）15x72
    （1）求表中x的值；
    （2）求这组数据的中位数和众数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

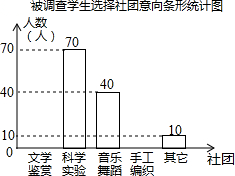    12．为了深化课程改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：
    某校被调查学生选择社团意向统计表
    选择意向文学鉴赏科学实验音乐舞蹈手工编织其他
    所占百分比a35%b10%c
    根据统计图表中的信息，解答下列问题：
    （1）求本次调查的学生总人数及a，b，c的值．
    （2）将条形统计图补充完整；
    （3）若该校共有1800名学生，试估计全校选择“科学实验”社团的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．大于-3且小于7的整数有哪几个？其中偶数有哪几个？

    查看答案和解析>>

    同步练习册答案