
分析 根据非负数的性质,列出关于a、b的方程组$\left\{\begin{array}{l}{4a-b+1=0}\\{\frac{1}{3}b-4a-3=0}\end{array}\right.$,通过解该方程组求得a、b的值,然后将其代入所求的代数式求值即可.
解答 解:由题意可得$\left\{\begin{array}{l}{4a-b+1=0}\\{\frac{1}{3}b-4a-3=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=-1}\\{b=-3}\end{array}\right.$.
当a=-1、b=-3时,原式=3•$\sqrt{\frac{1}{3}}$÷($\sqrt{3}$÷$\sqrt{\frac{1}{3}}$)=$\frac{\sqrt{3}}{3}$.
点评 本题综合考查了非负数的性质,算术平方根、解二元一次方程组、二次根式的性质等,利用非负数的性质得出a,b的值是解答此题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
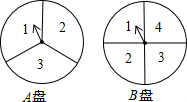 下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.
下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
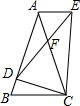 请完成下列的相似测试.
请完成下列的相似测试.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
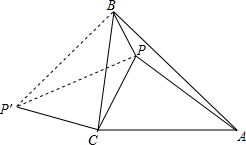 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com