
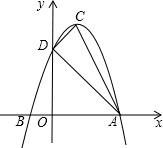
 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.分析 (1)由顶点坐标和A点坐标,可求得抛物线的解析式,容易求出B、D的坐标;
(2)根据点的坐标,利用勾股定理可求得AD、AC、CD的长,可判断△ACD的形状;
(3)先利用待定系数法求出直线AD的解析式,过点C作CE∥AD,求出直线CE的解析式,联立直线CE与抛物线的解析式即可得出E点坐标,在直线CD上截取CD=DF,求出F点的坐标,过点F作FG∥AD,利用待定系数法求出直线FG的解析式,联立此直线与抛物线的解析式即可得出E点坐标.
解答 解:(1)∵抛物线的顶点坐标为(1,4),
∴可设抛物线解析式为y=a(x-1)2+4,
∵与x轴交于点A(3,0),
∴0=4a+4,解得a=-1,
∴抛物线解析式为y=-(x-1)2+4=-x2+2x+3,
令y=0,可得-x2+2x+3=0,解得x=-1或x=3,令x=0,可得y=3
∴B点坐标为(-1,0),D点坐标为(0,3);
(2)∵A(3,0),D(0,3),C(1,4),
∴AD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,CD=$\sqrt{{(1-0)}^{2}+{(4-3)}^{2}}$=$\sqrt{2}$,AC=$\sqrt{(1-3)^{2}+(4-0)^{2}}$=2$\sqrt{5}$,
∴AD2+CD2=(3$\sqrt{2}$)2+($\sqrt{2}$)2=20=(2$\sqrt{5}$)2=AC2,
∴△ACD是以AC为斜边的直角三角形,
∴S△ACD=$\frac{1}{2}$AD•CD=$\frac{1}{2}$×3$\sqrt{2}$×$\sqrt{2}$=3;
(3)设直线AD的解析式为y=kx+b(k≠0),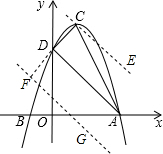
∵A(3,0),D(0,3),
∴$\left\{\begin{array}{l}3k+b=0\\ b=3\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=3\end{array}\right.$,
∴直线AD的解析式为y=-x+3.
过点C作CE∥AD,则直线CE的解析式为y=-x+c(a≠0),
∵C(1,4),
∴-1+c=4,解得c=5,
∴直线CE的解析式为y=-x+5,
∴$\left\{\begin{array}{l}y=-x+5\\ y=-{x}^{2}+2x+3\end{array}\right.$,解得$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,
∴E1(2,3);
设直线CD的解析式为y=mx+n(m≠0),
∵C(1,4),D(0,3),
∴$\left\{\begin{array}{l}4=m+n\\ 3=n\end{array}\right.$,解得$\left\{\begin{array}{l}m=1\\ n=3\end{array}\right.$,
∴直线CD的解析式为y=x+3.
∵CD=$\sqrt{(1-0)^{2}+(4-3)^{2}}$=$\sqrt{2}$,
∴DF=$\sqrt{2}$.
设F(x,x+3)且x<0,则DF=$\sqrt{{x}^{2}+{x}^{2}}$=$\sqrt{2}$,解得x=-1,
∴F(-1,2).
令直线FG的解析式为y=-x+d,则1+d=2,解得d=1,
∴直线FG的解析式为y=-x+1,
∴$\left\{\begin{array}{l}y=-x+1\\ y=-{x}^{2}+2x+3\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{3+\sqrt{17}}{2}\\ y=\frac{-1-\sqrt{17}}{2}\end{array}\right.$或$\left\{\begin{array}{l}x=\frac{3-\sqrt{17}}{2}\\ y=\frac{-1+\sqrt{17}}{2}\end{array}\right.$,
∴E2($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$),E3($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$).
综上所示,E1(2,3),E2($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$),E3($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$).
点评 本题考查的是圆的综合题,涉及到待定系数法及勾股定理的逆定理,根据抛物线的顶点坐标写出其顶点式求得抛物线的解析式是解题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | (a,$\sqrt{3}$a) | B. | (-a,-$\sqrt{3}$a) | C. | (-a,$\sqrt{3}$a) | D. | (-$\sqrt{3}$,a) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 捐款金额 | 5元 | 10元 | 15元 | 20元 | 50元 |
| 捐款人数 | 4人 | 12人 | 10 | 18人 | 6人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
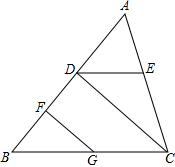 如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.
如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25π}{2}$厘米 | B. | 15π厘米 | C. | $\frac{75π}{2}$厘米 | D. | 75π厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
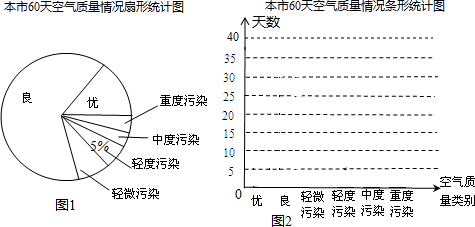
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 10 | a | 4 | b | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com