1．问题提出：有同样大小正方形256个，拼成如图1所示的16×16的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过多少个小正方形？
我们先考虑以下简单的情况：一条直线穿越一个正方形的情况．（如图2）
从图2中我们可以看出，当一条直线穿过一个小正方形时，这条直线最多与正方形上、下、左、右四条边中的两个边相交，所以当一条直线穿过一个小正方形时，这条直线会与其中某两条边产生两个交点，并且以两个交点为顶点的线段会全部落在小正方形内．
这就启发我们：为了求出直线L最多穿过多少个小正方形，我们可以转而去考虑当直线L穿越由小正方形拼成的大正方形时最多会产生多少个交点．然后由交点数去确定有多少根小线段，进而通过线段的根数确定下正方形的个数．
再让我们来考虑3×3正方形的情况（如图3）：为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个3×3的正方形，我们从两个方向来分析直线l穿过3×3正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的两条线段；从左右来看，这条直线最多可穿过左右平行的四条线段；这样直线L最多可穿过3×3的大正方形中的六条线段，从而直线L上会产生6个交点，这6个交点之间的5条线段，每条会落在一个不同的正方形内，因此直线L最多能经过5个小正方形．
问题解决：
（1）有同样大小的小正方形16个，拼成如图4所示的4×4的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过7个小正方形？
（2）有同样大小的小正方形100个，拼成10×10的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过19个小正方形？
（3）有同样大小的小正方形256个，拼成16×16的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过31个小正方形？
（4）请问如果用一条直线穿n×n大正方形的话，最多可以穿过2n-1个小正方形？
拓展探究：
（5）请问如果用一条直线穿2×3大长方形的话（如图5），最多可以穿过4个小正方形？
（6）请问如果用一条直线穿3×4大长方形的话（如图6），最多可以穿过6个小正方形？
（7）请问如果用一条直线穿m×n大长方形的话，最多可以穿过m+n-1个小正方形？
请将你的推理过程进行简要的叙述．
类比探究：由二维的平面我们可以联想到三维的立体空间，平面中的正方形中四条边可联想到正方体中的正方形的六个面，类比上面问题解决的方法解决如下问题．
（8）如图①有同样大小的小正方体8个，拼成如图①所示的2×2×2的一个大的正方体．请问如果用一条直线穿过这个大正方体的话，最多可以穿过多少个小正方体？
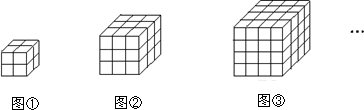
（9）请问如果用一条直线穿过n×n×n大正方体的话，最多可以穿过多少个小正方体？
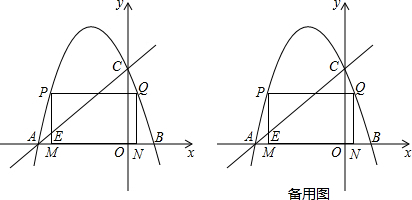
已知在∠MON中，A，B分别为ON，OM上一点．
长方体的主视图与俯视图如图所示，根据图中所示标尺寸，这个长方体的表面积为52．
一个立体图形的三视图如图所示，若π取3，请你根据图中给出的数据求出这个立体图形的体积为9．