
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

【答案】(1)见解析 (2)![]()
【解析】(1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,﹢根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,∠APD=90°,求出AP、DP,利用勾股定理求出PG,﹢根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
解:(1)如解图①所示,延长EB交DG于点H.

∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
∴△ADG≌△ABE(SAS), ∴∠AGD=∠AEB.
在△ADG中,∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°.
在△EDH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,即DG⊥BE
(2)如解图②,连结DG,过点A作AM⊥DG交DG于点M,
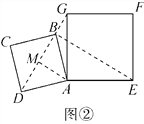
∠AMD=∠AMG=90°.
∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE.
在△ADG和△ABE中,
∴△ADG≌△ABE(SAS),∴DG=BE.
∵BD为正方形ABCD的对角线,∴∠MDA=45°.
在Rt△AMD中,∠MDA=45°,
∵AD=2,∴DM=AM=![]() ,
,
在Rt△AMG中,根据勾股定理得:
GM=![]() =
=![]() .
.
∵DG=DM+GM=![]() +
+![]() ,
,
∴BE=DG=![]() +
+![]()


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y与行驶时间x之间的函数图象.
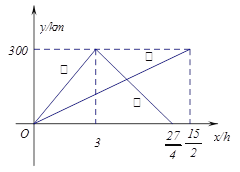
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量![]() 的取值范围;
的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)它们在行驶过程中有几次相遇.并求出每次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
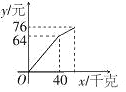
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
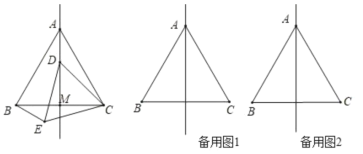
【题目】如图,在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE
(1)若点D在线段AM上时,求证:△ADC≌△BEC;
(2)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当动点D在线段AM的延长线上时,求当∠ACE为多少度时,点B、D、E在一条直线上;②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
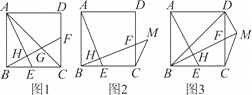
【题目】已知正方形ABCD中,点E,F分别为BC,CD上的点,连接AE,BF相交于点H,且AE⊥BF.
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点C,若AB=3,BC=1,则与圆环的面积最接近的整数是( )

A. 9 B. 10 C. 15 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商场经销一种高档水果,如果每千克盈利![]() 元,每天可售出
元,每天可售出![]() 千克.经市场调查发现,出售价格每降低
千克.经市场调查发现,出售价格每降低![]() 元,日销售量将增加
元,日销售量将增加![]() 千克.那么每千克应降价多少元,销售该水果每天可获得最大利润?最大利润是多少元?
千克.那么每千克应降价多少元,销售该水果每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com