
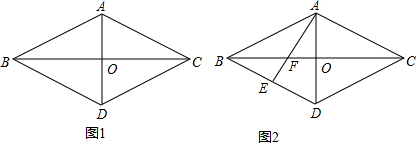
分析 (1)由△ABC≌△DBC,推出AB=BD,AC=CD,只要证明△ADB≌△ADC,推出AB=AC可得AB=BD=CD=AC即可证明.
(2)首先证明△ABD是等边三角形,即可判断.
解答 (1)证明:∵△ABC≌△DBC,
∴AB=BD,AC=CD,
∴∠BAD=∠BDA,∠CAD=∠CDA,
∵AD平分∠BAC,
∴∠DAB=∠DAC,∠ADC=∠ADC,
在△ADB和△ADC中,
$\left\{\begin{array}{l}{∠DAB=∠DAC}\\{AD=AD}\\{∠ADB=∠ADC}\end{array}\right.$,
∴△ADB≌△ADC,
∴AB=AC,
∴AB=BD=CD=AC,
∴四边形ABCD是菱形.
(2)解:∵∠AFO=∠ADC=∠ADB,
又∵∠AFO+∠EFO=180°,
∴∠EFO+∠EDO=180°,
∴∠FED+∠FOD=90°,
∵四边形ABCD是菱形,
∴AD⊥BC,
∴∠FEO=∠FOD=90°,
∵BE=ED,
∴AB=AD,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴∠EBF=$\frac{1}{2}$∠ABD=30°,
在Rt△BEF中,BF=2EF,
∵∠FBA=∠FAB=30°,
∴FA=FB,
在Rt△AFC中,CF=2AF=4EF,
综上所述,长度是线段EF长度的偶数倍的线段有BF,AF,CF.
点评 本题考查了菱形的判定和性质、等边三角形的判定和性质,直角三角形30度角性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若分式的分子为0时.则分式值为0 | B. | 分式的值总是分数 | ||
| C. | 分式的值也可能是整数 | D. | $\frac{71}{x}$的值可能是0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
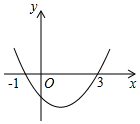 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1、3,则下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④对于任意x均有ax2-a+bx-b>0,其中正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1、3,则下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④对于任意x均有ax2-a+bx-b>0,其中正确的个数有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2400×(1-20%) | B. | 2400÷(1-20%) | C. | 2400×(1+20%) | D. | 2400÷(1+20%) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
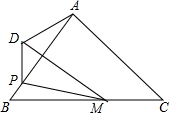 如图,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,则AD的最小值为$\sqrt{17}$-4.
如图,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,则AD的最小值为$\sqrt{17}$-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com