
| 矩形一边长/m | 5 | 10 | 15 | 20 |
| 矩形面积/m2 | 125 | 200 | 225 | 200 |
分析 (1)根据一边长及周长求出另一边长,再根据矩形面积公式计算可得;
(2)先表示出矩形的另一边长,再根据:矩形面积=长×宽,可得面积S关于l的函数解析式,配方成顶点式可得其最值情况;
(3)在以上函数解析式中令S=216,解方程可得l的值.
解答 解:(1)若矩形一边长为10m,则另一边长为$\frac{60}{2}$-10=20(m),此时矩形面积为:10×20=200(m2),
若矩形一边长为15m,则另一边长为$\frac{60}{2}$-15=15(m),此时矩形面积为:15×15=225(m2),
若矩形一边长为20m,则另一边长为$\frac{60}{2}$-20=10(m),此时矩形面积为:10×20=200(m2),
完成表格如下:
| 矩形一边长/m | 5 | 10 | 15 | 20 |
| 矩形面积/m2 | 125 | 200 | 225 | 200 |
点评 本题主要考查二次函数的实际应用能力,根据题意表示出另一边长是根本,将长乘以宽得出面积并配方找最大值是关键.


科目:初中数学 来源: 题型:解答题
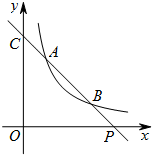 如图,已知直线y=ax+b与双曲线$y=\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
如图,已知直线y=ax+b与双曲线$y=\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
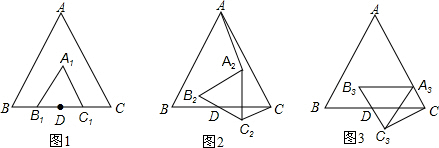 已知,△ABC和△A1B1C1均为正三角形,BC和B1C1的中点均为D,如图1.
已知,△ABC和△A1B1C1均为正三角形,BC和B1C1的中点均为D,如图1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
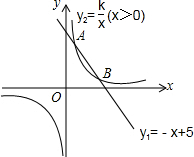 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com