
【题目】为加大环境保护力度,某市在郊区新建了![]() 、
、![]() 两个垃圾处理厂来处理甲、乙两个垃圾中转站的垃圾.已知甲中转站每日要输出100吨垃圾,乙中转站每日要输出80吨垃圾,
两个垃圾处理厂来处理甲、乙两个垃圾中转站的垃圾.已知甲中转站每日要输出100吨垃圾,乙中转站每日要输出80吨垃圾,![]() 垃圾处理厂日处理垃圾量为70吨,
垃圾处理厂日处理垃圾量为70吨,![]() 垃圾处理厂日处理垃圾量为110吨.甲、乙两中转站运往
垃圾处理厂日处理垃圾量为110吨.甲、乙两中转站运往![]() 、
、![]() 两处理厂的垃圾量和运费如下表.
两处理厂的垃圾量和运费如下表.
垃圾量(吨) | 运费(元/吨) | |||
甲中转站 | 乙中转站 | 甲中转站 | 乙中转站 | |
|
| ______ | 240 | 180 |
| ______ |
| 250 | 160 |
(1)设甲中转站运往![]() 垃圾处理厂的垃圾量为
垃圾处理厂的垃圾量为![]() 吨,根据信息填表.
吨,根据信息填表.
(2)设总运费为![]() 元,求总运费
元,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并写出
(吨)的函数关系式,并写出![]() 的取值范围.
的取值范围.
(3)当甲、乙两中转站各运往![]() 、
、![]() 两处理厂多少吨垃圾时,总运费最省?最省的总运费是多少?
两处理厂多少吨垃圾时,总运费最省?最省的总运费是多少?
【答案】(1)70-x,100-x;(2)y=![]() ;(3) 甲中转站运往
;(3) 甲中转站运往![]() 处理厂70吨垃圾,运往
处理厂70吨垃圾,运往![]() 处理厂30吨垃圾,乙中转站运往
处理厂30吨垃圾,乙中转站运往![]() 处理厂80吨垃圾,费用为37400元
处理厂80吨垃圾,费用为37400元
【解析】
(1) 根据题意写出关于x的式子即可
(2) 总运费为![]() 元,则
元,则 ![]() ,计算即可.
,计算即可.
(3) 根据已知![]() ,所以
,所以![]() 的值随
的值随![]() 的增大而减小,当
的增大而减小,当![]() 时,总运费
时,总运费![]() 最省.
最省.
(1)
垃圾量(吨) | 运费(元/吨) | |||
甲中转站 | 乙中转站 | 甲中转站 | 乙中转站 | |
|
| _ | 240 | 180 |
| _ |
| 250 | 160 |
(2)依题意有![]()
![]() .
.
(3)在上述一次函数中,![]() ,所以
,所以![]() 的值随
的值随![]() 的增大而减小.所以当
的增大而减小.所以当![]() 时,总运费
时,总运费![]() 最省,最省的总运费为37100元.即甲中转站运往
最省,最省的总运费为37100元.即甲中转站运往![]() 处理厂70吨垃圾,运往
处理厂70吨垃圾,运往![]() 处理厂30吨垃圾,乙中转站运往
处理厂30吨垃圾,乙中转站运往![]() 处理厂80吨垃圾.
处理厂80吨垃圾.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点![]() 点M不与B,C重合
点M不与B,C重合![]() ,
,![]() ,CN与AB交于点N,连接OM,ON,
,CN与AB交于点N,连接OM,ON,![]() 下列五个结论:
下列五个结论:![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() ∽
∽![]() ;
;![]() ;
;![]() 若
若![]() ,则
,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()
![]()

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
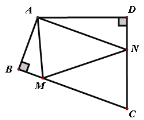
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的角度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离;
对应的点之间的距离;
例 1.解方程![]() ,因为在数轴上到原点的距离为
,因为在数轴上到原点的距离为![]() 的点对应的数为
的点对应的数为![]() ,所以方程
,所以方程![]() 的解为
的解为![]() .
.
例 2.解不等式![]() ,在数轴上找出
,在数轴上找出![]() 的解(如图),因为在数轴上到
的解(如图),因为在数轴上到![]() 对应的点的距离等于
对应的点的距离等于![]() 的点对应的数为
的点对应的数为![]() 或
或![]() ,所以方程
,所以方程![]() 的解为
的解为![]() 或
或![]() ,因此不等式
,因此不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
参考阅读材料,解答下列问题:
(1)方程![]() 的解为 ;
的解为 ;
(2)解不等式:![]() ;
;
(3)解不等式:.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=![]() BC,②
BC,②![]() ,③
,③![]() AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,B(0,6),A(8,0),以点B为旋转中心把△ABO逆时针旋转,得△A′BO′,点O,A旋转后的对应点为O′,A′,记旋转角为β.
(1)如图1,若β=90°,求AA′的长;
(2)如图2,若β=120°,求点O′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.

(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵数统计表 | ||||
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 | |

若经观测计算得出丙种树苗的成活率为89.6%,请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共 棵,乙品种树苗 棵;
(2)图1中,甲 %、乙 %,并将图2补充完整;
(3)求这次植树活动的树苗成活率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com