
【题目】如图1,已知直线PQ∥MN,点A、B分别在直线MN、PQ上,射线AM绕点A以5°/秒的速度按顺时针开始旋转,旋转至与AN(或AM)重合后便立即回转,射线BQ绕点B以2°/秒的速度按顺时针开始旋转,旋转至与BP重合后便停止转动,旋转后的射线分别记为AM'和BQ'.
(1)若射线BQ先转动30秒,射线AM才开始转动,在射线AM第一次到达AN之前,射线AM转动几秒后AM'∥BQ';
(2)若射线AM,BQ同时转动t秒,在射线BQ停止转动之前,记射线AM'与BQ'交于点H,若∠AHB=90°,求t的值;
(3)射线AM,BQ同时转动,在射线AM第一次到达AN之前,记射线AM'与BQ'交于点K,过K作KC⊥AK交PQ于点C,如图2,若∠BAN=30°,则在旋转过程中,∠BAK与∠BKC有何数量关系?并说明理由.

【答案】(1)t=10s时,BQ′∥AM′;(2)满足条件的t的值为30秒或90秒.(3)![]()
【解析】
(1)当∠MAM′=∠QBQ′时,BQ′∥AM′,延长构建方程即可解决问题;
(2)根据点Q的运动时间t=90秒,分三种情形分别构建方程求解即可;
(3)如图3中,设∠KAB=x,∠BKC=y.设直线CK交MN于G.利用平行线的性质,构建方程组确定x与y之间的关系即可.
(1)由题意当5t=30+2t时,BQ′∥AM′,
∴t=10s时,BQ′∥AM′.
(2)∵点Q的运动时间t=![]() =90(秒),
=90(秒),
分三种情形:①射线AM第一次到达AN之前:如图1中,

当∠NAM′+∠QBQ′=90°时,∠AHB=90°,
则有2t+180°﹣5t=90°,
解得t=30(秒),
②射线AM返回途中:如图2中,

当∠MAM′+∠PBQ′=90°时,∠AHB=90°,
则有180°﹣2t+180°﹣(5t﹣180°)=90°,
解得t=![]() (秒)(不合题意舍弃),
(秒)(不合题意舍弃),
③射线AM第二次到达AN之前,如图2中,
当∠MAM′+∠PBQ′=90°时,∠AHB=90°,
则有180°﹣2t+(5t﹣360°)=90°,
解得t=90(秒),
综上所述,满足条件的t的值为30秒或90秒.
(3)如图3中,设∠KAB=x,∠BKC=y.设直线CK交MN于G.

∵AK⊥KC,
∴∠AKG=90°,
∴∠KAG+∠AGK=90°,
∵PQ∥MN,
∴∠AGK=∠QCK,
∴180°﹣5t+2t+y=90°,
∴t=30°﹣![]() y,
y,
∵x=30°﹣(180°﹣5t),
∴x=5t﹣150°,
∴x=5(30°﹣![]() y)﹣150°,
y)﹣150°,
∴x=![]() y,
y,
∴∠KAB=![]() ∠BKC.
∠BKC.


科目:初中数学 来源: 题型:
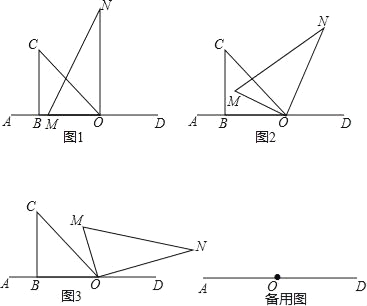
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题:
(1)若OA顺时针转动,OB逆时针转动,t= 秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB= °;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某边防局接到情报,近海处有一可疑船只![]() 正向公海方向行驶,边防局迅速派出快艇
正向公海方向行驶,边防局迅速派出快艇![]() 追赶(如图1).图2中
追赶(如图1).图2中![]() 、
、![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.
(分)之间的关系.
(1)求![]() 、
、![]() 的函数解析式;
的函数解析式;
(2)当![]() 逃到离海岸12海里的公海时,
逃到离海岸12海里的公海时,![]() 将无法对其进行检查.照此速度,
将无法对其进行检查.照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?若能,请求出此时
逃入公海前将其拦截?若能,请求出此时![]() 离海岸的距离;若不能,请说明理由.
离海岸的距离;若不能,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 km2;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com