
分析 根据抛物线y=2x2+bx+c与直线y=-1只有一个公共点,可知该抛物线顶点的纵坐标是-1,由A(m-1,n)和B(m+3,n),可得抛物线的对称轴和AB的长度,从而可以得到关于b,c的关系式,通过转化即可求得n的值,从而可以求得四边形AMNB的周长.
解答 解:y=2x2+bx+c=$2(x+\frac{b}{4})^{2}+c-\frac{{b}^{2}}{8}$,
∵抛物线y=2x2+bx+c与直线y=-1只有一个公共点,
∴$c-\frac{{b}^{2}}{8}=-1$,得$c=\frac{{b}^{2}}{8}-1$,
∵抛物线y=2x2+bx+c经过A(m-1,n)和B(m+3,n),
∴该抛物线的对称轴为:直线x=$\frac{m-1+m+3}{2}=m+1$=$-\frac{b}{2×2}=-\frac{b}{4}$,
∴b=-4(m+1),
∴$c=\frac{{b}^{2}}{8}-1=\frac{[-4(m+1)]^{2}}{8}-1$=2m2+4m+1,
∴y=2x2+bx+c=2x2-4(m+1)x+2m2+4m+1,
∴n=2×(m-1)2-4(m+1)(m-1)+2m2+4m+1=7,
即AM=BN=7,
∵A(m-1,n),B(m+3,n),
∴AB=(m+3)-(m-1)=4,
∴四边形AMNB的周长为是:AM+MN+NB+BA=7+4+7+4=22,
故答案为:22.
点评 本题考查二次函数的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


科目:初中数学 来源: 题型:选择题
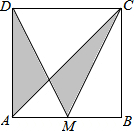 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
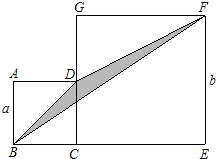 四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )| A. | ab | B. | $\frac{1}{2}$ab | C. | $\frac{1}{2}$b2 | D. | $\frac{1}{2}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
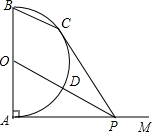 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).
如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,B,C,D为⊙O上的四个点,$\widehat{BC}$=$\widehat{CD}$,AC交BD于点E,CE=4,CD=6.
如图,点A,B,C,D为⊙O上的四个点,$\widehat{BC}$=$\widehat{CD}$,AC交BD于点E,CE=4,CD=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com