
分析 (1)根据二次根式的性质、绝对值的性质、立方根的概念计算;
(2)根据绝对值的性质和二次根式的加减运算法则计算;
(3)根据平方根的概念解答;
(4)根据立方根的概念计算.
解答 解:(1)(-$\sqrt{3}$)2-$\sqrt{\frac{1}{4}}$-$\root{3}{-0.125}$+$\sqrt{(-4)^{2}}$-|-6|
=3-$\frac{1}{2}$+$\frac{1}{2}$+4-6
=1;
(2)|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{3}$-2|
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$
=1;
(3)4(x+3)2-16=0
(x+3)2=4
x+3=±2
x=±2-3
x1=-5,x2=-1;
(4)27(x-3)3=-8
(x-3)3=-$\frac{8}{27}$
x-3=-$\frac{2}{3}$
x=$\frac{7}{3}$.
点评 本题考查的是实数的运算、平方根和立方根的概念,掌握实数的运算法则是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a2>b2,则a>b | B. | 若a>b,则a2>b2 | C. | 若|a|>b,则a2>b2 | D. | 若|a|≠|b|,则a2≠b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
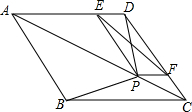 如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.
如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | $\frac{1}{4}$ | $\frac{1}{2}$ | 1 | 2 | 4 | 8 |
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象有公共点A(1,a)、D(-2,-1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象有公共点A(1,a)、D(-2,-1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com