
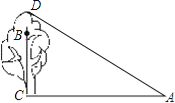
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
科目:初中数学 来源: 题型:
【题目】如果抛物线C: y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,那么m+n=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,
点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,![]() 的面积最大?求出
的面积最大?求出![]() 的最大面积及此时E点的坐标.
的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
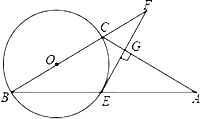
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )

A.nB.n﹣1C.![]() D.
D.![]() n
n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求直线![]() 的解析式;
的解析式;
(2)设点![]() 为直线
为直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 、
、![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,直线![]() 过直线
过直线![]() 与
与![]() 轴的交点
轴的交点![]() .设
.设![]() 的中点为
的中点为![]() ,
,![]() 是直线
是直线![]() 上一点,
上一点,![]() 是直线
是直线![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生会倡导的“爱心捐款”活动结束后,学生会干部对捐款情况作了抽样调查,并绘制了统计图,图中从左到右各长方形高度之比为![]() ,又知此次调查中捐15元和20元的人数共26人.
,又知此次调查中捐15元和20元的人数共26人.
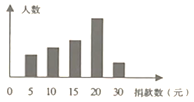
(1)他们一共抽查了______人;
(2)抽查的这些学生,总共捐款______元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com