
分析 根据同号得正、异号得负以及有理数的加法运算法则判断出a、b、c三个数中只有一个负数,然后求出x的值,再代入代数式进行计算即可得解.
解答 解:∵abc<0,且a+b+c>0,
∴a、b、c三个数中只有一个负数,两个正数,
不妨设a、b是正数,c是负数,
∴x=$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1+1-1=1,
∴x2008-2007x=12008-2007×1=1-2007=-2006.
故答案为:-2006.
点评 本题考查了代数式求值,有理数的乘法和加法运算,熟记运算法则并判断出三个数的正数、负数的个数是解题的关键.


科目:初中数学 来源: 题型:解答题
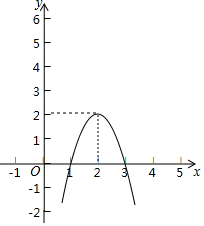 如图,二次函数y=-2(x-2)2+2的图象.
如图,二次函数y=-2(x-2)2+2的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com