
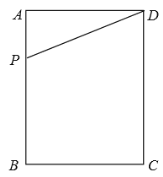
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连接DP,
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A,B处,若P,A,B三点恰好在同一直线上,且AB=2,试求此时AP的长.
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,请直接写出F到BC的距离.
【答案】(1)![]() 或
或![]() ;(2)1或3;(3)
;(2)1或3;(3)![]()
【解析】
(1)分两种情形:①当点![]() 在对角线
在对角线![]() 上时,设
上时,设![]() ,则
,则![]() ,利用勾股定理进行求解;②当点
,利用勾股定理进行求解;②当点![]() 在对角线
在对角线![]() 上时,利用相似三角形的性质进行求解;
上时,利用相似三角形的性质进行求解;
(2)设![]() ,则
,则![]() ,分两种情形分别构建方程进行求解;
,分两种情形分别构建方程进行求解;
(3)作FH⊥CD于H,作FI⊥BC于I,设BG=FG=x,在Rt△GCD中运用勾股定理得出x的值,根据FH∥CG求出FH的长,即可得出GI的长,最后在Rt△FGI中运用勾股定理进行求解.
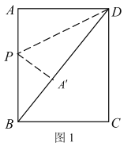
解:(1)①当点![]() 在对角线
在对角线![]() 上时,如图1,
上时,如图1,
![]() ,
,![]() ,
,
![]() ,
,
由折叠性质,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得,![]() ,
,
![]() ;
;
②当点![]() 在对角线
在对角线![]() 上时,如图2,
上时,如图2,
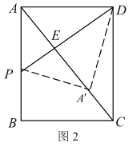
根据折叠的性质可知![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 长为
长为![]() 或
或![]() ;
;
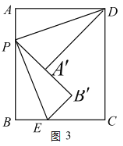
(2)①如图3,设![]() ,则
,则![]() ,根据折叠的性质可知:
,根据折叠的性质可知:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即![]() ,
,
②如图4,设![]() ,则
,则![]() ,
,
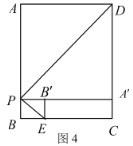
根据折叠性质可知:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即![]() ,
,
![]() 长为1或3;
长为1或3;
(3)如图5,作FH⊥CD于H,作FI⊥BC于I,
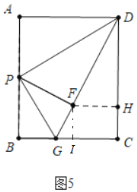
根据折叠性质可知:AD=DF=3,BG=GF,G、F、D三点共线,设BG=FG=x,
在Rt△GCD中,![]() ,
,
解得,![]() ,
,
∴DG=DF+FG=![]() ,CG=BC﹣BG=
,CG=BC﹣BG=![]() ,
,
∵FH∥CG,
∴![]() ,
,
∴![]() ,
,
∵易知四边形FICH为矩形,
∴FH=IC,
∴![]() ,
,
∴在Rt△FGI中,![]() ,
,
∴F到BC的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE;
(2)若∠BAC=30°,AB=12,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
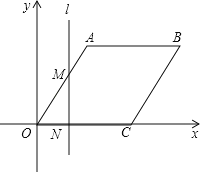
【题目】如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园音乐之声“结束后,王老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如下频数直方图和扇形统计图:
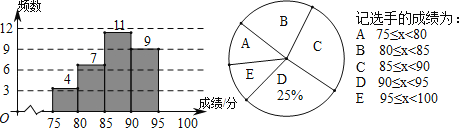
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形E的圆心角度数;
(3)成绩在E区域的选手中,男生比女生多一人,从中随机选取两人,求恰好选中两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
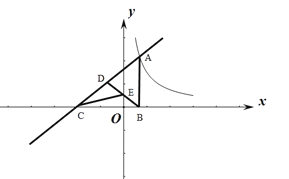
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)在(2)的条件下,已知点E为△ABC的重心,且OE=2,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
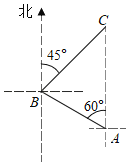
【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60方向行驶8千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点![]() ,有下列结论:
,有下列结论:
①abc![]() 0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c
0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c![]() 0; ⑤a﹣b≥m(am﹣b);
0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是______.(填写正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com