

分析 (1)设第n个三角形图案需要的火柴棍数为an(n为正整数)根,根据给定图形找出部分an的值,根据数的变化找出变化规律“an=$\frac{3n(n+1)}{2}$”,依此规律即可得出结论;
(2)根据(1)中规律解答即可.
解答 解:(1)n=1时,有1个三角形,需要火柴的根数为:3×1;
n=2时,有5个三角形,需要火柴的根数为:3×(1+2);
n=3时,需要火柴的根数为:3×(1+2+3)=18,
故答案为:18;
(2)根据(1)中规律,当n=10时,需要火柴的根数为3×(1+2+3+…+10)=165,
故答案为:165.
点评 本题考查了规律型中的图形的变化类,解题的关键是根据火柴棍数目的变化找出变化规律“an=$\frac{3n(n+1)}{2}$”是解题的关键.


科目:初中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| x2-2x-2 | -3 | -2 |
| x | 2.6 | 2.7 | 2.8 | 2.9 |
| x2-2x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,b>0 | B. | a>0,b<0,|a|>|b| | C. | a<0,b>0,|a|<|b| | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
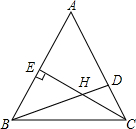 如图,在△ABC中,∠ABC=50°,∠ACB=70°,BD是∠ABC的平分线,CE是AB边上的高线,BD与CE交于点H,求∠ADB和∠BHC的度数.
如图,在△ABC中,∠ABC=50°,∠ACB=70°,BD是∠ABC的平分线,CE是AB边上的高线,BD与CE交于点H,求∠ADB和∠BHC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,点C在线段AB上,线段AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长?
(1)如图,点C在线段AB上,线段AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com