
 按照图示的方式可以将一张正方形纸片拆成一个环保纸袋(如图所示).
按照图示的方式可以将一张正方形纸片拆成一个环保纸袋(如图所示). ,则折成后纸袋的边AE和HI的长分别为________、________.
,则折成后纸袋的边AE和HI的长分别为________、________.
 6-4
6-4
 -x,在直角△EFD中利用勾股定理即可得到一个关于x的方程,解方程求得AE的长;
-x,在直角△EFD中利用勾股定理即可得到一个关于x的方程,解方程求得AE的长;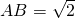 ,
, AB=2,
AB=2, -x,
-x, EF,即
EF,即 -x=
-x= x,解得:x=2-
x,解得:x=2- ,
, ;
; AE=
AE= (2-
(2- )=2
)=2 -2,
-2, -2,
-2, -2)=6-4
-2)=6-4 .
. ,6-4
,6-4 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com