
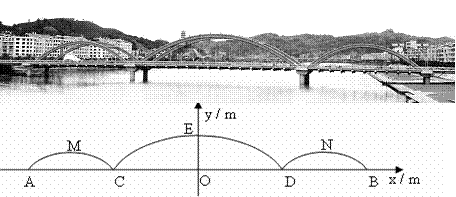
许多桥梁都采用抛物线型设计,小明将他家乡的彩虹桥按比例缩小后,绘成如下的示意图,图中的三条抛物线分别表示桥上的三条钢梁,x轴表示桥面,y轴经过中间抛物线的最高点,左右两条抛物线关于y轴对称.经过测算,中间抛物线的解析式为:y=- x2+10,并且BD=
x2+10,并且BD= CD.
CD.

(1)求钢梁最高点离桥面的高度OE的长;
(2)求桥上三条钢梁的总跨度AB的长;
(3)若拉杆DE∥拉杆BN,求右侧抛物线的解析式.
(1)10m;(2)80m;(3)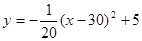
【解析】
试题分析:(1)将x=0代入抛物线的解析式就可以直接求出结论.(2)当y=0时代入抛物线的解析式,求出其交点坐标就可以求出CD的长度,从而就可以BD、CD的值而得出结论.(3)由(2)的结论可以求出点B、点D的坐标,作NF⊥x轴于点F,连结DE、BN,△NFB∽△EOD就可以求出NF的值而得出N的坐标,再由待定系数法就可以求出结论.
试题解析:(1)在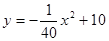 中,当x=0时,y=10,
中,当x=0时,y=10,
∴钢梁最高点离桥面的高度OE的长10m;
(2)在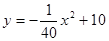 中,当y=0时,
中,当y=0时, ,解得x=±20,
,解得x=±20,
∴C(-20,0),D(20,0),
∴DC=40,
∵BD=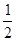 CD,
CD,
∴BD=20,
∵左右两条抛物线关于y轴对称,
∴AC=BD=20,
∴AB=40+20+20=80m;
(3)作NF⊥x轴于点F,连结DE、BN
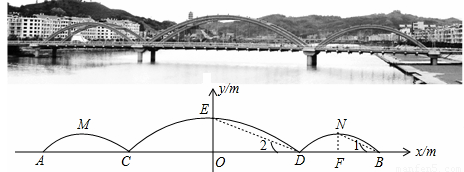
∴∠NFB=∠EOD=90°,DF=BF=10,
∵DE∥BN,
∴∠2=∠1,
∴△NFB∽△EOD,
∴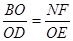 ,
,
∴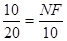 ,
,
∴NF=5.
∴N(30,5).
设抛物线的解析式为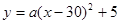 ,由题意得
,由题意得
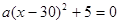 ,解得
,解得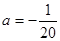
∴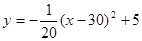 .
.
考点:二次函数的应用


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
| 1 |
| 40 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 x2+10,并且BD=
x2+10,并且BD= CD.
CD.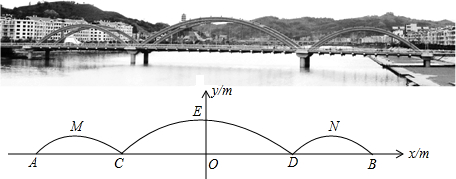
查看答案和解析>>
科目:初中数学 来源: 题型:
许多桥梁都采用抛物线型设计,小明将他家乡的彩虹桥按比例缩小后,绘成如下的示意图,图中的三条抛物线分别表示桥上的三条钢梁,x轴表示桥面,y轴经过中间抛物线的最高点,左右两条抛物线关于y轴对称。经过测算,中间抛物线的解析式为
y=-![]() x2+10,并且BD=
x2+10,并且BD=![]() CD。
CD。
(1)求钢梁最高点离桥面的高度OE的长;
(2)求桥上三条钢梁的总跨度AB的长;
(3)若拉杆DE∥拉杆BN,求右侧抛物线的解析式。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com