
 某校一大楼AB的高为18米,不远处有一水塔CD.某同学在楼底A处测得塔顶D处的仰角为62°,在楼顶B点测得塔顶D处仰角为38°.求CD的高度(结果精确到0.1米)( 参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
某校一大楼AB的高为18米,不远处有一水塔CD.某同学在楼底A处测得塔顶D处的仰角为62°,在楼顶B点测得塔顶D处仰角为38°.求CD的高度(结果精确到0.1米)( 参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78) 分析 首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△DBE、△ABC,应利用其中BE=AC的等量关系,进而可求出答案.
解答 解:如图,设DE=x米.
在Rt△BDE中,
∵tan38°=$\frac{ED}{BE}$,
∴$\frac{x}{BE}$≈0.78,
∴BE≈$\frac{x}{0.78}$,
∵四边形ACED是矩形,
∴AC=BE≈$\frac{x}{0.78}$,CE=AB=18,
在Rt△AFC中,
∵tan62°=$\frac{DC}{AC}$,
∴$\frac{x+18}{\frac{x}{0.78}}$≈1.88,
解得,x≈12.8,
∴DC=DE+CE≈12.8+18=30.8(米).
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两条船同时从A港出发,一艘船的速度是15海里/时,航向是东北方向,另一艘船比它每小时快5海里,航向是东南方向,多少小时后两船相距100海里?
两条船同时从A港出发,一艘船的速度是15海里/时,航向是东北方向,另一艘船比它每小时快5海里,航向是东南方向,多少小时后两船相距100海里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
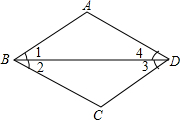 已知,如图,AB∥CD,BC∥AD,∠3=∠4,求证:∠1=∠2.
已知,如图,AB∥CD,BC∥AD,∠3=∠4,求证:∠1=∠2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com