
����Ŀ��ij�̳�ͳ����ÿ��ӪҵԱ��ij�µ����۶ͳ��ͼ���£�����ͳ��ͼ�и�������Ϣ������������⣺
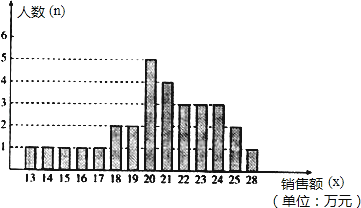
��1����ӪҵԱ�������۶�Ϊx����λ����Ԫ�����̳��涨����x��15ʱΪ����ְ����15��x��20ʱ��Ϊ������ְ����20��x��25Ϊ��ְ����x��25ʱΪ���㣮��ְ�������ӪҵԱ���ж����ˣ���ռ�ٷֱ��Ƕ��٣�
��2�����ݣ�1���й涨�����г�ְ���ϣ�ְ�ƺ����㣩��ӪҵԱ�����۶����λ����������ƽ�����ֱ��Ƕ��٣�
��3��Ϊ�˵���ӪҵԱ�Ĺ��������ԣ������ƶ������۶��������������������ӪҵԱ���ܵ����������Ҫʹ�ó�ְ���ϣ���ְ�����㣩��ӪҵԱ��һ���ܻ�����Ϊ���������Ӧ�������۶�Ϊ����Ԫ���ʣ������������ɣ�
���𰸡���1����������3�ˣ���ְ����18�ˣ���ռ�ٷֱ�Ϊ![]() ��100%=70%����2����λ����22��Ԫ��������20��Ԫ��ƽ������22
��100%=70%����2����λ����22��Ԫ��������20��Ԫ��ƽ������22![]() ����Ԫ������3�����������Ӧ�������۶�Ϊ22��Ԫ���ʣ�
����Ԫ������3�����������Ӧ�������۶�Ϊ22��Ԫ���ʣ�
��������
�����������1�����������ְ��������ӪҵԱ�������������ݰٷֱȵ�������⣻
��2��������λ����������ƽ�����������ɣ�
��3�����Ҫʹ�ó�ְ��������������ε�����ӪҵԱ�İ��������ܻ������۶�������Զ�Ϊ��ְ������������������۶����λ������Ϊ��λ�����ϵ�����ռ��������һ�����ң�
�⣺��1����ͼ��֪ӪҵԱ��������Ϊ2+1=3���ˣ���
��ͼ��֪ӪҵԱ������Ϊ1+1+1+1+1+2+2+5+4+3+3+3+2+1=30���ˣ���
���ְ����18�ˣ���ռ�ٷֱ�Ϊ![]() ��100%=70%��
��100%=70%��
��2����λ����22��Ԫ��
������20��Ԫ��
ƽ�����ǣ�![]() =22
=22![]() ����Ԫ����
����Ԫ����
��3�����������Ӧ�������۶�Ϊ22��Ԫ���ʣ�
��Ϊ��ְ���ϵ�ӪҵԱ�����۶����λ����22��Ԫ��˵�����۶�ﵽ�ͳ���22��Ԫ��ӪҵԱռ��ְӪҵԱ��һ�룬����ʹ��ְ����ӪҵԱ��һ���ܻ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M=(x��3)(x��7)��N=(x��2)(x��8)����M��N�Ĺ�ϵΪ�� ��
A. M��N B. M��N C. M=N D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�ס�A��B��C�䣬��A=20�㣬��C=120�㣬���B��Ķ���Ϊ�� ��
A.20��
B.30��
C.40��
D.120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ������֤������320919197807051995�����֪������ʦ�������ǣ�_____��____��_____�գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����O�ǵȱ�������ABC��һ�㣬��֪��AOB=130������BOC=125�����������߶�OA��OB��OCΪ�߹��ɵ��������У��ڽDz�����ȡ���ĽǶ��ǣ� ��
A��65�� B��60�� C��45�� D��70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ1����һ�β������ֱ��ӳ�AB,BC,CA����A1,B1,C1,ʹA1B=AB,B1C=BC,C1A=CA,˳������A1,B1,C1,�õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1=A1B1��B2C1=B1C1��C2A1=C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2017�����پ������������β�����
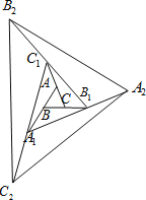
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ������AOBC��λ��ͼ��ʾ����OAC=90�㣬AC��OB��OA=4��AC=5��OB=6��M��N�ֱ����߶�AC���߶�BC���˶�������MON������ﵽ���ʱ������һ��ʹ����MON�ܳ���С����������ʱ��M������Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ��A��B���ҳ��з��������е�ѧϰ��������ĵ��۶���ͬ��ѧϰ��������ĵ���֮��Ϊ452Ԫ����ѧϰ���ĵ��۱�������۵�4����8Ԫ��
��1��ѧϰ��������ĵ��۸��Ƕ���Ԫ��
��2����ͬѧ�Ͻ֣�ǡ�ø��ϸ���Ʒ����������A������Ʒ��������ۣ�����Bȫ������100Ԫ������ȯ30Ԫ���ۣ���200Ԫ������ȯ60Ԫ���������ƣ�������100Ԫ����ȯ������ȯȫ��ͨ�ã�������ֻ����390ԪǮ�������ֻ��һ�ҳ��й��������е���������Ʒ������˵��������ѡ���ļҹ����ʡǮ��?
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com