
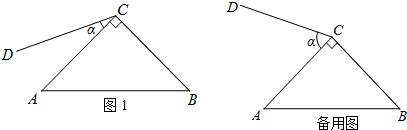
分析 (1)由题意补全图形,如图1所示,
(2)先判断出△BCD≌△ACE,再判断出∠2=∠4,从而得到∠1+∠2=90°,即得到结论;
(3)先判断出当α=64°时GH的长度最大,然后计算出∠DBA=32°,∠GAB=58°再在表示出AH,BH用AH+BH=4建立方程求解即可.
解答 解:(1)补全图形,如图1所示.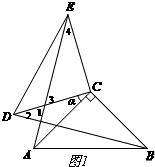
(2)AE与BD的数量关系:AE=BD,
AE与BD的位置关系:AE⊥BD.
证明:∵∠ACB=∠DCE=90°,
∴∠ACB+α=∠DCE+α.
即∠BCD=∠ACE.
∵BC=AC,CD=BC,
∴△BCD≌△ACE.
∴AE=BD.
∴∠4=∠CBD.
∵∠CBD=∠2,
∴∠2=∠4.
∵∠3+∠4=90°,∠1=∠3,
∴∠1+∠2=90°.
即AE⊥BD.
(3)如图2,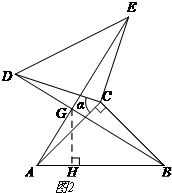
过点G作GH⊥AB于H.
由线段CD的运动可知,当α=64°时GH的长度最大.
∵CB=CD,
∴∠CBD=∠CDB,
∴∠CBD=$\frac{180°-90°-64°}{2}$=13°,
∴∠DBA=32°.
由(2)可知,∠AGB=90°,
∴∠GAB=58°,
在Rt△GAH中,tan∠GAB=tan58°=$\frac{GH}{AH}$,
∴AH=$\frac{GH}{tan58°}$,
在Rt△GBH中,tan∠DBA=tan32°=$\frac{GH}{BH}$,
∴BH=$\frac{GH}{tan32°}$,
∵AB=4,
∴AH+BH=4,
∴$\frac{GH}{tan58°}$+$\frac{GH}{tan32°}$=4,
∴GH=2(tan58°+tan32°).
点评 此题是几何变换综合题,主要考查了三角形全等的判定和性质,判断线垂直的方法,锐角三角函数,判断AE⊥BD,AE=BD是解本题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:选择题
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
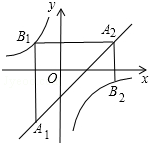 如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.
如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
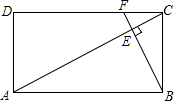 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
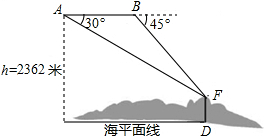 国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
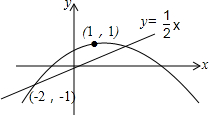 如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:
如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com