
分析 根据分子分母同乘以有理化因式进行分析整理.
解答 解:$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{3-2}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=$\frac{2-\sqrt{3}}{4-3}$=2-$\sqrt{3}$;
$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\frac{\sqrt{5}-2}{5-4}$=$\sqrt{5}$-2.
$\frac{1}{3+\sqrt{10}}$=$\frac{\sqrt{10}-3}{(\sqrt{10}+3)(\sqrt{10}-3)}$=$\frac{\sqrt{10}-3}{10-9}$=$\sqrt{10}$-3.
故答案是:$\sqrt{3}$-$\sqrt{2}$;2-$\sqrt{3}$;$\sqrt{5}$-2;$\sqrt{10}$-3.
点评 主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:填空题
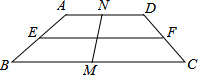 如图,在梯形ABCD中AD∥BC,∠B=40°,∠C=50°,E、M、F、N分别是边AB、BC、CD、DA的中点,且EF=a,MN=b,则BC的长为a+b.
如图,在梯形ABCD中AD∥BC,∠B=40°,∠C=50°,E、M、F、N分别是边AB、BC、CD、DA的中点,且EF=a,MN=b,则BC的长为a+b.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.
如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com