
【题目】如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )

A. 5对; B. 4对; C. 3对; D. 2对
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE.
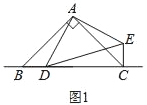
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
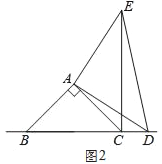
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
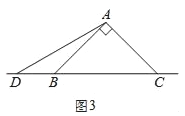
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
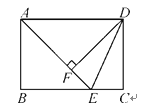
【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年元月,国内一家网络诈骗举报平台发布了《2015年网络诈骗趋势研究报告》,根据报告提供的数据绘制了如下的两幅统计图: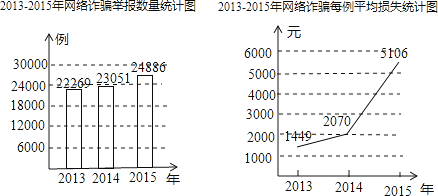
(1)该平台2015年共收到网络诈骗举报多少例?
(2)2015年通过该平台举报的诈骗总金额大约是多少亿元?(保留三个有效数字)
(3)2015年每例诈骗的损失年增长率是多少?
(4)为提高学生的防患意识,现准备从甲、乙、丙、丁四人中随机抽取两人作为受骗演练对象,请用树状图或列表法求恰好选中甲、乙两人的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算 1+3+5+7+9+11;
(2)请计算 1+3+5+7+9+…+19;
(3)请计算 1+3+5+7+9+…+(2n﹣1);
(4)请用上述规律计算:21+23+25+…+99.

查看答案和解析>>
科目:初中数学 来源: 题型:
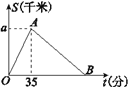
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图像提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次过C点到第二次过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.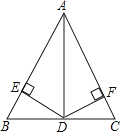
(1)求证:AB=AC;
(2)若AD=2 ![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com