
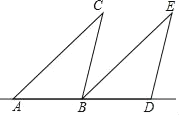
【题目】如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移![]() 格,再纵向平移
格,再纵向平移![]() 格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么
格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么![]() 的结果( )
的结果( )

A.只有一个确定的值B.有两个不同的值
C.有三个不同的值D.有三个以上不同的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在数轴上表示的数是﹣6,点B表示的数是+10,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴做匀速运动,设运动时间为t(秒).
(1)线段AB的长度为 个单位;
(2)如果点P向右运动,点Q向左运动,求:
①当t为何值时,P与点Q相遇?
②当t为何值时,PQ=![]() AB?
AB?
(3)如果点P,点Q同时向左运动,是否存在这样的时间t使得P,Q两点到A点距离相等?若存在,求出t的值,若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有一![]() ,且
,且![]() ,
,![]() ,
,![]() ,已知
,已知![]() 是由
是由![]() 绕某点顺时针旋转得到的.
绕某点顺时针旋转得到的.

(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出![]() 顺时针旋转90°、180°的三角形;
顺时针旋转90°、180°的三角形;
(3)设![]() 两直角边
两直角边![]() 、
、![]() 、斜边
、斜边![]() ,利用变换前后所形成的图案验证勾股定理.
,利用变换前后所形成的图案验证勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1,2,3,...,30,这30个整数,任意分为15组,每组2个数.现将每组数中的一个数记为![]() ,另一个数记为
,另一个数记为![]() ,计算代数式
,计算代数式![]() 的值,15组数代入后可得到15个值,则这15个值之和的最小值为( )
的值,15组数代入后可得到15个值,则这15个值之和的最小值为( )
A.![]() B.120C.225D.240
B.120C.225D.240
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华同学经过调查,了解到某客车租赁公司有![]() ,
,![]() 两种型号的客车,并得到了下表中的信息.
两种型号的客车,并得到了下表中的信息.
车型 |
|
|
|
| |
座位 | 45座 | 60座 |
信息 | 每辆 | |
5辆 | ||
(1)求每辆![]() 型和
型和![]() 型客车每天的租金各是多少元?
型客车每天的租金各是多少元?
(2)小华所在学校准备组织七年级全体学生外出一天进行研学活动,小华同学设计了下面甲乙两种租车方案:
方案甲:只租用![]() 型客车,但有一辆客车会空出30个座位.
型客车,但有一辆客车会空出30个座位.
方案乙:只租用![]() 型客车,刚好坐满,且比方案甲少用两辆客车.
型客车,刚好坐满,且比方案甲少用两辆客车.
求小华所在学校七年级学生的总人数.
(3)如果从节省费用的角度考虑,是否还有其他租车方案?如果有,请直接写出一种租车方案;如果没有,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2x2﹣4x+1=0(配方法)
(2)﹣3x=1﹣x2
(3)2(x+2)2=x(x+2)
(4)(x+1)(x﹣1)+2(x+3)=8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AD为△ABC的中线,过B、C两点分别作AD所在直线的垂线段BE和CF,E、F为垂足,过点E作EG∥AB交BC于点H,连结HF并延长交AB于点P。
(1)求证:DE=DF
(2)若![]() ;①求:
;①求:![]() 的值;②求证:四边形HGAP为平行四边形。
的值;②求证:四边形HGAP为平行四边形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com