练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．当x=$\frac{5}{2}$时，代数式2x-3的值与-|-$\frac{1}{2}$|互为负倒数．

    分析 根据负倒数的定义列出方程求出x的值即可．

    解答 解：由题意可知：（2x-3）×（-|-$\frac{1}{2}$|）=-1
    ∴（2x-3）×（-$\frac{1}{2}$）=-1
    ∴2x-3=2
    ∴x=$\frac{5}{2}$，
    故答案为：$\frac{5}{2}$

    点评 本题考查一元一次方程，解题的关键是根据题意列出方程，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．有这样一个问题：探究函数y=$\frac{1}{x}$+1的图象与性质．
    小明根据学习一次函数的经验，对函数y=$\frac{1}{x}$+1的图象与性质进行了探究．
    下面是小明的探究过程，请补充完整：
    （1）函数y=$\frac{1}{x}$+1的自变量x的取值范围是x≠0；
    （2）下表是y与x的几组对应值．
    x…-4-3-2-1-mm1234…
    y…$\frac{3}{4}$$\frac{2}{3}$$\frac{1}{2}$0-132$\frac{3}{2}$$\frac{4}{3}$$\frac{5}{4}$…
    求出m的值；
    （3）如图，在平面直角坐标系xOy中，描出了以表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
    （4）写出该函数的一条性质该函数没有最大值或 该函数没有最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如果a、b为定值时，关于x的方程$\frac{2kx+a}{3}$=2+$\frac{x-bk}{6}$，无论k取何值时，它的根总是1，则a=$\frac{13}{2}$，b=-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若不等式5（x-2）+8≤6（x-1）+7的最小整数解是方程3x-ax=-3的解，求4a-$\frac{14}{a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

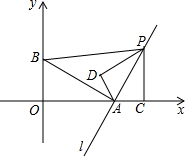    12．如图，在直角坐标系中，点A（2，0），点B（0，1），过点A的直线l垂直于线段AB，点P是直线l上一动点，过点P作PC⊥x轴，垂足为C，把△ACP沿AP翻折180°，使点C落在点D处．若以A，D，P为顶点的三角形与△ABP相似，则所有满足此条件的点P的坐标为P（5，2），p（8，8），P（0，-8），P（3，-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，△ABC为等边三角形，边长为2，AB与x轴平行，顶点C坐标为（2，$\sqrt{3}$+1），规定把等边△ABC“先沿x轴翻折，再向右平移1个单位”为一次变换，如果这样连续经过3次变换后，等边△ABC的顶点A的坐标为（4，-1），如果这样连续经过2017次变换后，等边△ABC的顶点A的坐标为（2018，-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

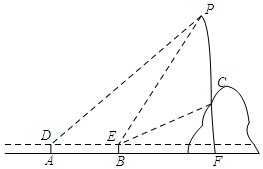    9．如图，从水平地面看一山坡上的通讯铁塔PC，在点A处用测角仪测得塔顶端点P的仰角是45°，向前走9m到达B点，用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°．
    （1）求∠BPC的度数．
    （2）求该铁塔PF的高度，（结果精确到0.1m，参考数据：$\sqrt{3}≈1.73$．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知点A（a，2），B（-3，b）关于y轴对称，则ab=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．设m，n是方程x2-x-2013=0的两个实数根．则m2+n的值为2014．

    查看答案和解析>>

    同步练习册答案