
【题目】如图,O是等边![]() 内一点,
内一点,![]() ,以点B为旋转中心,将线段BO逆时针旋转
,以点B为旋转中心,将线段BO逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() 可以由
可以由![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得到
得到
②连接![]() ,则
,则![]()
③![]()
④![]()
其中正确的结论是____________.
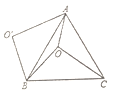
【答案】①②③
【解析】
如图,连接OO′,首先证明△OBO′为为等边三角形,得到OO′=OB=4,故选项②正确;证明△ABO′≌△CBO,得到选项①正确;运用勾股定理逆定理证明△AOO′为直角三角形,求出∠AOB的度数,得到选项③正确;运用三角函数及三角形面积公式求出四边形AOBO′的面积,可判断选项④错误.
解:如图,连接OO′;
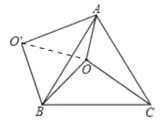
∵△ABC为等边三角形,
∴∠ABC=60°,AB=CB,
由题意得:∠OBO′=60°,OB=O′B,
∴△OBO′为等边三角形,∠ABO′=∠CBO,
∴OO′=OB=4,∠BOO′=60°,②正确;
在△ABO′与△CBO中,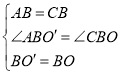 ,
,
∴△ABO′≌△CBO(SAS),
∴AO′=OC=5,
∴△BO′A可以由△BOC绕点B逆时针方向旋转60°得到,①正确;
在△AOO′中,AO′=5,OA=3,OO′=4,
∵32+42=52,
∴△AOO′为直角三角形,且∠AOO′=90°,
∴∠AOB=90°+60°=150°,③正确;
∵S四边形AOBO′=![]() ×4×4×sin60°+
×4×4×sin60°+![]() ×3×4=
×3×4=![]() ,④错误,
,④错误,
综上所述,正确的结论为①②③.
故答案为:①②③.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的图象经过点A(﹣1,0),B(0,﹣3).
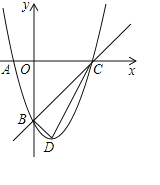
(1)求这个抛物线的解析式;
(2)抛物线与x轴的另一交点为C,抛物线的顶点为D,判断△CBD的形状;
(3)直线BN∥x轴,交抛物线于另一点N,点P是直线BN下方的抛物线上的一个动点(点P不与点B和点N重合),过点P作x轴的垂线,交直线BC于点Q,当四边形BPNQ的面积最大时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
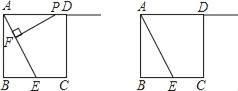
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(3)试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知函数
中(如图),已知函数![]() 的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
(1)求反比例函数的解析式;
(2)把直线![]() 平移后与
平移后与![]() 轴相交于点B,且
轴相交于点B,且![]() ,求平移后直线的解析式.
,求平移后直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
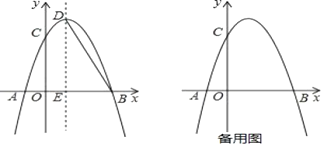
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是
是![]() 轴上方抛物线上的动点,以
轴上方抛物线上的动点,以![]() 为边作正方形
为边作正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小、位置也随着改变,当顶点
的运动,正方形的大小、位置也随着改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,请直接写出点
轴上时,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.
(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;
(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=![]() ,求线段AH长
,求线段AH长

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com