
分析 (1)根据题意,可以设每张门票的原定的票价是x元,然后根据按原定票价需花费6000元购买门票,现在只花了4000元即可列出方程,本题得以解决;
(2)根据题意,可以列出相应的方程,注意要使平均每天的个人票收入达到241500元,且能有效控制游览人数,则说明在获得这些利润时,游客越少越容易控制.
解答 解:(1)设每张门票的原定的票价是x元,
$\frac{6000}{x}=\frac{4000}{x-40}$
解得,x=120
经检验x=120是原分式方程的解,
即每张门票的原定的票价是120元;
(2)要使平均每天的个人票收入达到241500元,且能有效控制游览人数,则票价应降低x元,
(120-x)(2000+$\frac{x}{2}$×40)=241500,
解得,x1=5,x2=15,
∵能有效控制游览人数,
∴x=5时,购买的人数较少,可以较好的控制,
即要使平均每天的个人票收入达到241500元,且能有效控制游览人数,则票价应降低5元.
点评 本题考查一元二次方程的应用,解答此类问题的关键是明确题意,列出相应的方程,注意在(1)中的分式方程要检验,(2)中要联系实际情况.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,点A、B、C对应的数分别为a、b、c,下列说法:①若a+b+c=0,则D为原点;②若|c|>|a|>|b|,则原点在B、D之间;③若c-b=8,则a-b=-2;④若原点在D、E之间,则|a+b|<2c,其中正确的结论有( )
如图,数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,点A、B、C对应的数分别为a、b、c,下列说法:①若a+b+c=0,则D为原点;②若|c|>|a|>|b|,则原点在B、D之间;③若c-b=8,则a-b=-2;④若原点在D、E之间,则|a+b|<2c,其中正确的结论有( )| A. | ①②③ | B. | ①③ | C. | ③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
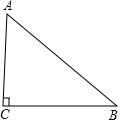 如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.
如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com