
分析 如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,此时△PQ′R′的周长最小,这个最小值=P′P″,再证明P′P″=2MN,MN最小时,△PQR周长最小,利用图2证明当点P与点D重合时MN最小,在图3中利用相似三角形的性质求出MN的最小值即可解决问题.
解答 解:如图1中,
作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,
此时△PQ′R′的周长最小,这个最小值=P′P″,
∵PM=MP′,PN=NP″,
∴P′P″=2MN,
∴当MN最小时P′P″最小.
如图2中,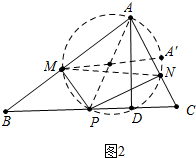
∵∠AMP=∠ANP=90°,
∴A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,
∵∠MAN是定值,
∴直径AP最小时,弦MN最小,
∴当点P与点D重合时,PA最小,此时MN最小.
如图3中,
∵在RT△ABD中,∠ADB=90°,AD=2,DB=3,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{13}$,
在RT△ADC中,∵∠ADC=90°,AD=2,CD=1,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{5}$,
∵DM⊥AB,DN⊥AC,
∴$\frac{1}{2}$•AC•DN=$\frac{1}{2}$•DC•AD,
∴DN=$\frac{2}{\sqrt{5}}$,AN=$\sqrt{A{D}^{2}-D{N}^{2}}$=$\frac{4\sqrt{5}}{5}$,
∵∠MAD=∠DAB,∠AMD=∠ADB,
∴△AMD∽△ADB,
∴$\frac{AM}{AD}$=$\frac{AD}{AB}$,
∴AD2=AM•AB,同理AD2=AN•AC,
∴AM•AB=AN•AC,
∴$\frac{AM}{AC}$=$\frac{AN}{AB}$,
∵∠MAN=∠CAB,
∴△AMN∽△ACB,
∴$\frac{MN}{BC}$=$\frac{AN}{AB}$,
∴$\frac{MN}{4}$=$\frac{\frac{4\sqrt{5}}{5}}{\sqrt{13}}$,
∴MN=$\frac{16\sqrt{65}}{65}$,
∴△PQR周长的最小值=P′P″=2MN=$\frac{32\sqrt{65}}{65}$.
故答案为$\frac{32\sqrt{65}}{65}$.
点评 此题主要考查了轴对称-最短问题、圆、相似三角形的判定和性质等知识,根据两点之间线段最短的知识找到P点的位置是解答此题的关键,题目比较难,属于中考填空题中的压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
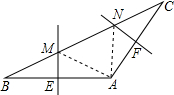 在△ABC中,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.
在△ABC中,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的三个顶点别为A(1,4),B(5,1),C(1,9),若双曲线y=$\frac{k}{x}$(x>0)在第一象限内与△ABC有交点,求k的取值范围.
如图,△ABC的三个顶点别为A(1,4),B(5,1),C(1,9),若双曲线y=$\frac{k}{x}$(x>0)在第一象限内与△ABC有交点,求k的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
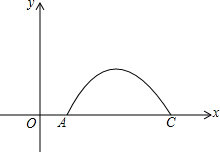 如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒,当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小王骑自行车通过拱梁部分的桥面AC供需26秒.
如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒,当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小王骑自行车通过拱梁部分的桥面AC供需26秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com