
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.
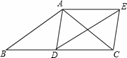
解答: 证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
 ,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴▱ADCE是矩形.



科目:初中数学 来源: 题型:
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A. 24 B. 18 C. 16 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。每件商品降价多少元时,商场日盈利可达到2 100元
100元 ?为获得最大利润,商场该商品应降价多少元?
?为获得最大利润,商场该商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
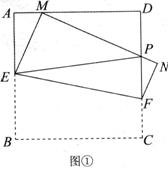
如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
(1)如图②,若M为AD边的中点,
①△AEM的周长=__ ___cm;
②求EP的长;
(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在下列条件中,能证明△ABD≌△ACD的是 .(填序号)
①BD=DC,AB=AC; ②∠ADB=∠ADC,BD=DC ;
③∠B=∠C,∠BAD=∠CAD; ④∠B=∠C,BD=DC.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com