
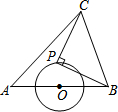
 如图,AB=4,O为AB的中点,⊙O的半径为1,点P是⊙O上一动点,以PB为直角边的等腰直角三角形PBC(点P、B、C按逆时针方向排列),则线段AC的长的取值范围为$\sqrt{2}$≤AC≤3$\sqrt{2}$.
如图,AB=4,O为AB的中点,⊙O的半径为1,点P是⊙O上一动点,以PB为直角边的等腰直角三角形PBC(点P、B、C按逆时针方向排列),则线段AC的长的取值范围为$\sqrt{2}$≤AC≤3$\sqrt{2}$. 分析 如图,作OK⊥AB,在OK上截取OK=OA=OB,连接AK、BK、KC、OP.首先证明△OBP∽△KBC,得$\frac{KC}{OP}$=$\frac{BC}{PB}$=$\sqrt{2}$,由OP=1,推出KC=$\sqrt{2}$,所以点C的运动轨迹是以点K为圆心,KC为半径的圆,由此即可解决问题.
解答 解:如图,作OK⊥AB,在OK上截取OK=OA=OB,连接AK、BK、KC、OP.
∵OK=OA=OB,OK⊥AB,
∴KA=KB,∠AKB=90°,
∴△AKB是等腰直角三角形,
∵∠OBK=∠PBC,
∴∠OBP=∠KBC,
∵$\frac{OB}{BK}$=$\frac{PB}{BC}$=$\frac{\sqrt{2}}{2}$,
∴△OBP∽△KBC,
∴$\frac{KC}{OP}$=$\frac{BC}{PB}$=$\sqrt{2}$,∵OP=1,
∴KC=$\sqrt{2}$,
∴点C的运动轨迹是以点K为圆心,KC为半径的圆,
AK=$\sqrt{2}$OA=2$\sqrt{2}$,
∴AC的最大值为3$\sqrt{2}$,AC的最小值$\sqrt{2}$,
∴$\sqrt{2}$≤AC≤3$\sqrt{2}$.
故答案为$\sqrt{2}$≤AC≤$3\sqrt{2}$.
点评 本题考查圆综合题、相似三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,解题的突破点是发现点C的运动轨迹是以点K为圆心,KC为半径的圆,所以中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
 如图,小龙在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小龙的前后身高相同(即PE=QF),两个路灯的高度相同(即AC=BD)
如图,小龙在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小龙的前后身高相同(即PE=QF),两个路灯的高度相同(即AC=BD)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
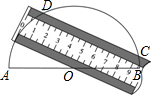 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 19cm或11cm | B. | 19cm或14cm | C. | 11cm 或14cm | D. | 19cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com