

分析 (1)由正方形的性质得到∠ABC=90°,根据切线的判定即可证得结论;
(2)设OB=OM=x.则AO=4-x,AM=2,根据勾股定理得x2=22+(4-x)2,解方程即可求得结论;
(3)如图,作BP⊥MN于点P,根据切线的想知道的∠PMB=$\frac{1}{2}$∠MOB,∠CBM=$\frac{1}{2}$∠MOB,根据平行线的性质得到∠CBM=∠AMB,于是得到∠AMB=∠PMB,根据切线的性质得到AM=MP,BP=AB=BC,PN=CN,于是得到结论.
解答 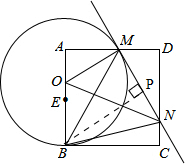 解:(1)∵正方形ABCD,
解:(1)∵正方形ABCD,
∴∠ABC=90°,
∵OB为半径,
∴BC是⊙O的切线;
(2)∵正方形ABCD,
∴∠A=90°,AB=AD=4,
∵M是AD的中点,
设OB=OM=x.则AO=4-x,AM=2,
在Rt△AOM中,x2=22+(4-x)2,
解得:x=$\frac{5}{2}$,
∴OB=$\frac{5}{2}$时,⊙O经过AD的中点;
(3)如图,作BP⊥MN于点P,
∵MN,BC是⊙O的切线,
∴∠PMB=$\frac{1}{2}$∠MOB,∠CBM=$\frac{1}{2}$∠MOB,
∵AD∥BC,
∴∠CBM=∠AMB,
∴∠AMB=∠PMB,
在Rt△MAB和Rt△MPB中,
$\left\{\begin{array}{l}{∠BPM=∠BAM}\\{∠PMB=∠AMB}\\{BM=BM}\end{array}\right.$
∴Rt△MAB≌Rt△MPB(AAS)
∴AM=MP,BP=AB=BC,
在Rt△BPN和Rt△BCN中,
$\left\{\begin{array}{l}{BP=BC}\\{BN=BN}\end{array}\right.$
∴Rt△BPN≌Rt△BCN(HL)
∴PN=CN,
MN=MP+PN=AM+CN,
∴DM+DN+MN=DM+DN+AM+CN=(AM+DM)+(DN+CN)=AD+DC=8,
故△DMN的周长是一个定值8.
点评 本题是圆的综合题目,考查了切线的性质和判定、正方形的性质、勾股定理,方程,全等三角形的判定与性质等知识;本题主要考查了圆的切线及全等三角形的判定和性质,关键是作出辅助线利用三角形全等证明.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=α度,∠2=β度,则( )
如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=α度,∠2=β度,则( )| A. | α+β=150 | B. | α+β=90 | C. | α+β=60 | D. | β-α=30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165,165 | B. | 165,170 | C. | 170,165 | D. | 170,170 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com