
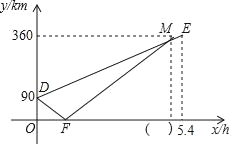
����Ŀ��A��B��C������ͬһ����·�ϣ�A����B��C����֮�䣬�ס�������ͬʱ��A�س���������ʻ���׳�ʻ��C�أ��ҳ���ʻ��B�أ�����B�غ�ͷ��ԭ�پ���A��ʻ��C�أ���ͷʱ����Բ��ƣ�������C��ֹͣ��ʻ���׳����ҳ���0.4Сʱ����C�أ�������B�ص�·��y��km������ʻʱ��x��h��֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ������������⣺
��1���׳���ʻ���ٶ����� ��km/h������ͼ��������������ȷ����ֵ��
��2����ͼ�����߶�FM����ʾ��y��x�ĺ�������ʽ������Ҫд���Ա���x��ȡֵ��Χ����
��3�����ҳ�����C��֮ǰ���ס�������������Сʱ��A��·����ȣ�ֱ��д���𰸣�
���𰸡���1��50��5����2��y��90x��90��1��x��5��;��3��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��
��������
��1���۲�ͼ���ҳ�A��C���ؼ�ľ��룬�ٸ����ٶȣ�·����ʱ�䣬��������׳���ʻ���ٶȣ��ɼ׳����ҳ���0.4Сʱ����C�ؽ�ϼ׳�5.4Сʱ����C�أ��ɵó��ҳ�����C������ʱ�䣻
��2�������ٶȣ�·����ʱ�������ҳ����ٶȣ���ʱ�䣽·�����ٶȿɵó���F�ĺ����꣬�ٸ���·�̣��ٶ�����ʱ�䩁1�������ɵó��߶�FM����ʾ��y��x�ĺ�������ʽ��
��3������·�̣��ٶ���ʱ�䣨·�̣�90���ٶ���ʱ�䣩���ɵó��߶�DM��DF������ʾ��y��x�ĺ�������ʽ����0��x��1�Լ�1��x��5����������ҳ�����x��һԪһ�η��̣���֮���ɵó����ۣ�
�⣺��1��A��C���ؼ�ľ���Ϊ360��90��270��km����
�׳���ʻ���ٶ�Ϊ270��5.4��50��km/h����
�ҳ��ﵽC������ʱ��Ϊ5.4��0.4��5��h����
�ʴ�Ϊ��50��5��
��2���ҵ��ٶ�Ϊ��90+360����5��90��km/h����
��F�ĺ�����Ϊ90��90��1��
���߶�FM����ʾ��y��x�ĺ�������ʽΪy��90��x��1����90x��90��1��x��5����
��3���߶�DE����ʾ��y��x�ĺ�������ʽΪy��50x+90��0��x��5.4����
�߶�DF����ʾ��y��x�ĺ�������ʽΪy��90��90x��0��x��1����
��0��x��1ʱ����90����90��90x����50x+90��90��
��ã�x��0����ȥ����
��1��x��5ʱ����|90x��90��90|��50x+90��90��
��ã�![]()
�����ҳ�����C��֮ǰ���ס�������������![]() Сʱ��
Сʱ��![]() Сʱ��A��·����ȣ�
Сʱ��A��·����ȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
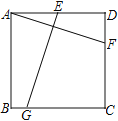
����Ŀ����ͼ���ڱ߳�Ϊ6��������ABCD�У���FΪCD��һ�㣬E��AD���е㣬��DF��2����BC���ҵ�G��ʹEG��AF����BG�ij���___________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
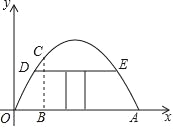
����Ŀ����һ�����������߲˴��������������ͼ��ʾ��ƽ��ֱ������ϵ�У������߿����ú���y��ax2+bx����ʾ����֪OA��8�ף�����O��2�״������BCΪ![]() �ף�
�ף�
��1����������ߵĽ���ʽ��
��2������������DE��DE��OA����һ���ţ�Ҫ���ŵĸ߶�Ϊ1.5�ף������DE�ij����Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
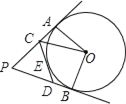
����Ŀ����֪��PA��PB��CD�ֱ��С�O��A��B��E���㣬PA��6����
��1����PCD���ܳ���
��2������P��50�������COD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
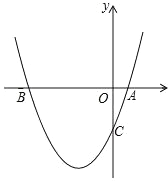
����Ŀ����ͼ����֪���κ��� y��x2+bx+c ���� A��1��0����C��0����3��
��1����˶��κ����Ľ���ʽ��
��2�����ABC �������
��3�����������ϴ���һ�� P ʹ��ABP �����Ϊ 10��������� P �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪRt��ABC��ֱ�DZ�AC��һ�㣬��OCΪ�뾶��Բ��б��AB�����ڵ�D��P�ǻ�CD������һ�㣬����P����O�����ߣ���BC�ڵ�M����AB�ڵ�N����֪AB��5��AC��4��
��1����BMN���ܳ����ڶ�����
��2����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ�����ʾ��
x | �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
y | �� | ��6 | 0 | 4 | 6 | 6 | �� |
����˵��������������y��Ľ���Ϊ��0��6���� �������ߵĶԳ�����y����Ҳࣻ��������һ�������㣨3��0�������ڶԳ�����࣬y��x�������С��������ʽax2+��b��3��x+c��6��0�⼯Ϊ��2��x��0������˵����ȷ���У�������
A. 1 �� B. 2 �� C. 3 �� D. 4 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ң���ABC�͡�ADE���й�������ĵ���ֱ�������Σ���BAC=��DAE=90������PΪ����BD��CE�Ľ��㣮
��1����ͼ�ף�����ADE�Ƶ�A ��ת����C��D��E��ͬһ��ֱ����ʱ������BD��BE�������и������ĸ������У�������ȷ����_____��
��BD=CE��BD��CE�ۡ�ACE+��DBC=45����BE2=2��AD2+AB2��
��2����AB=4��AD=2���ѡ�ADE�Ƶ�A��ת��
�ٵ���EAC=90��ʱ����PB�ij���
������ת�������߶�PB�������ֵ��
 ����
���� ������
������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ��![]() ����2�����ݵ�x��
����2�����ݵ�x��![]() ʱ��y��x���������С����a+b+c��0���߷���ax2+bx+c����4��ʵ���⣬��ȷ������ ��
ʱ��y��x���������С����a+b+c��0���߷���ax2+bx+c����4��ʵ���⣬��ȷ������ ��
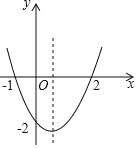
A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com