Question

14．如图1，已知点A（0，-3）和x轴上的动点C（m，0），△AOB和△BCD都是等边三角形．
（1）在C点运动的过程中，始终有两点的距离等于OC的长度，请将它找出来，并说明理由．
（2）如图2，将△BCD沿CD翻折得△ECD，当点C在x轴上运动时，设点E（x，y），请你用m来表示点E的坐标并求出点E运动时所在图象的解析式．
（3）在C点运动的过程中，当m＞$\sqrt{3}$时，直接写出△ABD是等腰三角形时E点的坐标．

Answer 1

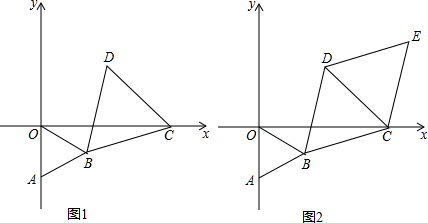
分析 （1）连接AD，根据等边三角形的性质可得出“AB=OB，BD=BC，∠ABO=∠CBD=60°”，再通过角的计算得出∠ABD=∠OBC，由此即可证出△ABD≌△OBC，根据全等三角形的性质即可得出AD=OC；
（2）过D作DF⊥y轴于F，连接BE，由（1）中的△ABD≌△OBC结合等边三角形的性质即可得出点D的坐标，由△AOB为等边三角形结合点A、O的坐标即可得出点B的坐标，由翻折的性质可得出四边形BCED是菱形，再根据菱形的性质结合点B、C、D的坐标即可得出点E的坐标，根据点E坐标的横纵坐标之间的关系即可得出结论；
（3）由（2）可知点B、D、A的坐标，结合两点间的距离公式可得出BD的长，再根据等腰三角形的性质分三种情况，可得出关于m的方程，解方程求出m的值，代入点E的坐标即可得出结论．

解答 解：（1）连接AD，如图1所示．

A、D两点间的距离始终等于OC的长度．理由如下：
∵△AOB和△BCD都是等边三角形，
∴AB=OB，BD=BC，∠ABO=∠CBD=60°，
∵∠ABD=∠ABO+∠OBD，∠OBC=∠OBD+∠DBC，
∴∠ABD=∠OBC．
在△ABD和△OBC中，有$\left\{\begin{array}{l}{AB=OB}\\{∠ABD=∠OBC}\\{BD=BC}\end{array}\right.$，
∴△ABD≌△OBC（SAS），
∴AD=OC．
（2）过D作DF⊥y轴于F，连接BE，如图2所示．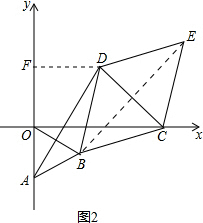

由（1）可知△ABD≌△OBC，
∴AD=OC=m，∠DAF=∠BAO-∠BAD=60°-（90°-60°）=30°
∴DF=AD•sin∠DAF=$\frac{1}{2}$m，AF=AD•cos∠DAF=$\frac{\sqrt{3}}{2}$m，
∵A（0，-3），
∴D（$\frac{1}{2}$m，$\frac{\sqrt{3}}{2}$m-3）．
∵将△BCD沿CD翻折得△ECD且△BCD是等边三角形，
∴四边形BCED是菱形，
∴BE、CD互相平分．
∵△AOB是等边三角形，且点O（0，0），点A（0，-3），
∴点B（$\frac{3\sqrt{3}}{2}$，-$\frac{3}{2}$），
∴E（$\frac{3}{2}$m-$\frac{3}{2}$$\sqrt{3}$，$\frac{\sqrt{3}}{2}$m-$\frac{3}{2}$）．
∵$\frac{\sqrt{3}}{2}$m-$\frac{3}{2}$=$\frac{\sqrt{3}}{3}$（$\frac{3}{2}$m-$\frac{3}{2}$$\sqrt{3}$），
∴点E在图形y=$\frac{\sqrt{3}}{3}$x上运动．
（3）∵点A（0，-3），点B（$\frac{3\sqrt{3}}{2}$，-$\frac{3}{2}$），点D（$\frac{1}{2}$m，$\frac{\sqrt{3}}{2}$m-3），
∴AB=3，AD=m，BD=$\sqrt{（\frac{1}{2}m-\frac{3\sqrt{3}}{2}）^{2}+[\frac{\sqrt{3}}{2}m-3-（-\frac{3}{2}）]^{2}}$=$\sqrt{{m}^{2}-3\sqrt{3}m+9}$，
△ABD为等腰三角形分三种情况：
①当AB=AD时，有3=m，
此时点E的坐标为（$\frac{9}{2}$-$\frac{3}{2}$$\sqrt{3}$，$\frac{3}{2}$$\sqrt{3}$-$\frac{3}{2}$）；
②当AB=BD时，有3=$\sqrt{{m}^{2}-3\sqrt{3}m+9}$，
解得：m=0（舍去），或m=3$\sqrt{3}$，
此时点E的坐标为（3$\sqrt{3}$，3）；
③当AD=BD时，有m=$\sqrt{{m}^{2}-3\sqrt{3}m+9}$，
解得：m=$\sqrt{3}$（舍去）．
综上可知：在C点运动的过程中，当m＞$\sqrt{3}$时，△ABD是等腰三角形时E点的坐标为（$\frac{9}{2}$-$\frac{3}{2}$$\sqrt{3}$，$\frac{3}{2}$$\sqrt{3}$-$\frac{3}{2}$）或（3$\sqrt{3}$，3）．

点评 本题考查了等边三角形的性质、全等三角形的判定及性质、特殊角的三角函数值、两点间的距离公式以及一次函数图象上点的坐标特征，解题的关键是：（1）证出△ABD≌△OBC；（2）求出点E的坐标；（3）分三种情况求点E的坐标．本题属于中档题，难度不大，但较繁琐，解决该题型题目时，熟练的掌握等边三角形和菱形的性质是解题的关键．