
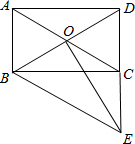
 如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.分析 (1)根据矩形的对角线相等可得AC=BD,对边平行可得AB∥CD,再求出四边形ABEC是平行四边形,根据平行四边形的对边相等可得AC=BE,从而得证;
(2)如图,过点O作OF⊥CD于点F,欲求tan∠OED的值,只需在直角△OEF中求得OF、FE的值即可.OF结合三角形中位线求得,EF结合矩形、平行四边形的性质以及勾股定理求得即可.
解答 解:(1)∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE;
(2)如图,过点O作OF⊥CD于点F,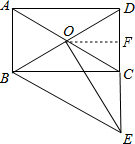 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BCD=90°.
∵BE=BD=10,
∴CD=CE=6.
同理,可得CF=DF=$\frac{1}{2}$CD=3,
∴EF=9.
在直角△BCE中,由勾股定理可得:BC=8.
∵OB=OD,
∴OF为△BCD的中位线,
∴OF=$\frac{1}{2}$BC=4,
∴在直角△OEF中,tan∠OED=$\frac{OF}{EF}$=$\frac{4}{9}$.
点评 本题考查了矩形的性质,平行四边形的判定与性质,熟记各性质并求出四边形ABEC是平行四边形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查你班同学的年龄情况 | B. | 为订购校服,了解学生衣服的尺寸 | ||
| C. | 考察一批炮弹的杀伤半径 | D. | 对航天飞机上的零部件进行检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 检查一枚用于发射卫星的运载火箭的各零部件 | |
| D. | 考察人们保护海洋的意识 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题


查看答案和解析>>
科目:初中数学 来源: 题型:填空题
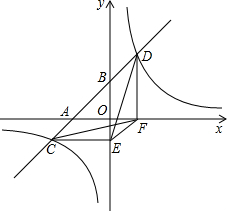 如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com