
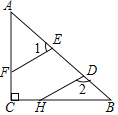
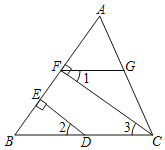
【题目】如图,D,E为△ABC边AB上两点,F,H分别在AC,BC上,∠1+∠2=180°
(1)求证:EF∥DH;
(2)若∠ACB=90°,∠DHB=25°,求∠EFC的度数.
【答案】(1)见解析;(2)∠EFC=115°.
【解析】
(1)由∠1+∠2=180°,∠ADH+∠2=180°,得出∠1=∠ADH,即可得出结论;
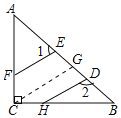
(2)过点C作CG∥DH,交AB于G,则∠GCB=∠DHB=25°,推出∠ACG=∠ACB﹣∠GCB=65°,由EF∥DH,得出CG∥EF,得出∠EFC+∠ACG=180°,即可得出结果.
(1)证明:∵∠1+∠2=180°,∠ADH+∠2=180°,
∴∠1=∠ADH,
∴EF∥DH;
(2)解:过点C作CG∥DH,交AB于G,如图所示:
则∠GCB=∠DHB=25°,
∴∠ACG=∠ACB﹣∠GCB=90°﹣25°=65°,
由(1)得:EF∥DH,
∴CG∥EF,
∴∠EFC+∠ACG=180°,
∴∠EFC=180°﹣∠ACG=180°﹣65°=115°.


科目:初中数学 来源: 题型:
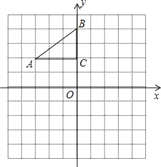
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
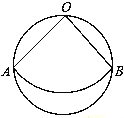
【题目】如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,将理由补充完整.
如图,CF⊥AB于F,DE⊥AB于E,∠1+∠EDC=180°,求证:FG∥BC
证明:∵CF⊥AB,DE⊥AB(已知)
∴∠BED=∠BFC=90°(垂直的定义)
∴ED∥FC ( )
∴∠2=∠3 ( )
∵∠1+∠EDC=180°(已知)
又∵∠2+∠EDC=180°(平角的定义)
∴∠1=∠2 ( )
∴∠1=∠3(等量代换)
∴FG∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com