
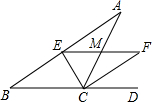
 如图,在三角形ABC中,CE平分∠ACB,CF平分∠ACD且EF∥BC交AC于点M,若EF=3,则CE2+CF2=36.
如图,在三角形ABC中,CE平分∠ACB,CF平分∠ACD且EF∥BC交AC于点M,若EF=3,则CE2+CF2=36. 分析 根据角平分线的定义、外角定理推知∠ECF=90°,然后在直角三角形ECF中利用勾股定理求CE2+CF2的值即可.
解答 解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=$\frac{1}{2}$∠ACB,∠ACF=$\frac{1}{2}$∠ACD,即∠ECF=$\frac{1}{2}$(∠ACB+∠ACD)=90°,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=3,EF=6,
由勾股定理可知CE2+CF2=EF2=36,
故答案为36.
点评 本题考查了直角三角形的性质,平行线的性质,以及角平分线的定义,证明出△ECF是直角三角形是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
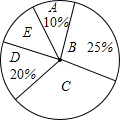 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.| 组别 | A | B | C | D | E |
| 时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
| 人数 | 12 | 30 | a | 24 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
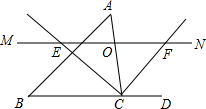 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.求证:OE=OF.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.求证:OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
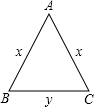 如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm)
如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
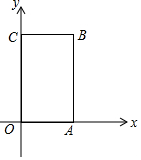 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com