
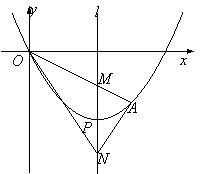
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
【答案】(1)![]()
(2)12
(3)相似三角形的基本知识推出该角度的相等,不能
【解析】
试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为![]() 。
。
又∵二次函数图象经过原点(0,0),∴![]() ,解得
,解得![]() 。
。
∴二次函数的关系式为![]() ,即
,即![]() 。(2分)
。(2分)
(2)设直线OA的解析式为![]() ,将A(6,-3)代入得
,将A(6,-3)代入得![]() ,解得
,解得![]() 。
。
∴直线OA的解析式为![]() 。
。
把x=4代入![]() 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。
又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴![]() 。(3分)
。(3分)
(3)①证明:过点A作AH⊥![]() 于点H,,
于点H,,![]() 与x轴交于点D。则
与x轴交于点D。则
设A(![]() ),
),
则直线OA的解析式为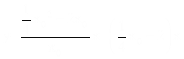 。
。
则M(![]() ),N(
),N(![]() ),H(
),H(![]() )。
)。
∴OD=4,ND=![]() ,HA=
,HA=![]() ,NH=
,NH=![]() 。
。
∴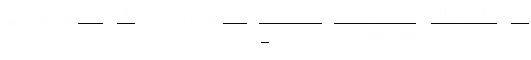 。
。
∴![]()
![]() 。∴∠ANM=∠ONM。(2分)
。∴∠ANM=∠ONM。(2分)
②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则![]() 。
。
∵![]() ,
,
∴![]() 。
。
整理,得![]() ,解得
,解得![]() ,
,![]() 。
。
∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴![]() 。
。
∵OD=4,MD=![]() ,ND=
,ND=![]() ,∴
,∴![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴![]() 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】2019年5月16日,第十五届文博会在深圳拉开帷幕,周末,小明骑共享单车从家里出发去分会馆参观,途中突然发现钥匙不见了,于是原路折返,在刚才等红绿灯的路口找到了钥匙,便继续前往分会馆,设小明从家里出发到分会场所用的时间为x(分钟),离家的距离为y(米),且x与y的关系示意图如图所示,请根据图中提供的信息回答下列问题:
(1)图中自变量是 .因变量是 .
(2)小明等待红绿灯花了 分钟.
(3)小明的家距离分会馆 米
(4)小明在 时间段的骑行速度最快,最快速度是 米/分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________;
(2)求同时满足下列条件的所有“和平数”:
①个位上的数字是千位上的数字的两倍;
②百位上的数字与十位上的数字之和是12的倍数;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.
例如:1423于4132为“相关和平数”
求证:任意的两个“相关和平数”之和是1111的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
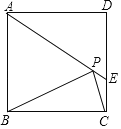
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林的门票每张10元,一次使用,考虑到人们的不同需求,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购买日起,可供持票者使用一年).年票分A、B、C三类:A类年票每张120元,持票者进入园林时,无需再用门票;B类年票每张60元,持票者进入该园林时,需再购买门票,每次2元;C类年票每张40元,持票者进入该园林时,需再购买门票,每次3元.
(1)如果只选择一种购买门票的方式,并且计划在一年中用不多于80元花在该园林的门票上,试通过计算,找出可进入该园林次数最多的购票方式,
(2)一年中进入该园林至少超过______________次时,购买A类年票最合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com