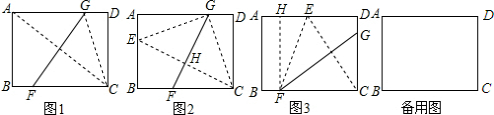
解:(1)连接CG.
∵点C与点A关于FG对称,
∴FG垂直平分AC,
∴∠AHG=90°,AH=

AC=2.5.
在△AHG与△CBA中,∵∠AHG=∠CBA,∠GAH=∠ACB,
∴△AHG∽△CBA,
∴HG:AB=AH:BC,
∴HG=3×2.5÷4=

.
在△AHG与△CHF中,
∠GAH=∠HCF,AH=CH,∠AHG=∠CHF,
∴△AHG≌△CHF,
∴HG=HF,
∴FG=2HG=

;
(2)连接CG,EG,则FG垂直平分CE.
在△CHF与△CBE中,∠CHF=∠B=90°,∠HCF=BCE,
∴△CHF∽△CBE,
∴HF:BE=CH:BC,
∴CH=2HF.
设HF=x,则CE=2CH=4x.
在△BCE中,∠B=90°,
∴CE
2=BE
2+BC
2,
∴16x
2=4+16,
∴x=

.
设DG=y,则AG=4-y.
∵GE=GC,
∴1
2+(4-y)
2=3
2+y
2,
∴y=1.
∴GC
2=DG
2+CD
2=1+9=10,
∴GH
2=GC
2-CH
2=10-5=5,
∴GH=

,
∴GF=GH+HF=

+

=
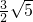
;
(3)过点F作FH⊥AD,H为垂足,连接FE.则FE=FC=4-y,HE=x-y,FH=3,
由勾股定理有(x-y)
2+3
2=(4-y)
2,
从而得
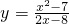
(1<x<

);
(4)AB、AD、BC.
故答案为

;
;AB、AD、BC.
分析:(1)连接CG,可证△AHG∽△CBA,根据相似三角形的对应边成比例可求出HG的长度;易证△AHG≌△CHF,则FG=2HG;
(2)连接CG,EG,则FG垂直平分CE.易证△CHF∽△CBE,得出CH=2HF.在直角△BCE中,运用勾股定理,可出CE的长度,求出HF的值;设DG=y,由GE=GC,运用勾股定理求出y的值,得到CG的长度,从而在直角△CHG中,由勾股定理计算出GH的值,则GF=GH+HF;
(3)过点F作FH⊥AD,H为垂足,连接FE.在直角△HFE中,运用勾股定理可求得y关于x的函数解析式,并根据条件得到函数的定义域;
(4)(2)中点C与点E重合,且DG=1,即点E可以在边AB上,同样,可知点E可以在边AD、BC上.
点评:本题考查了轴对称、矩形的性质,全等三角形、相似三角形的判定与性质及勾股定理等知识,综合性较强,有一定难度.


 AC=2.5.
AC=2.5. .
. ;
;
 .
. ,
, +
+ =
=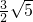 ;
;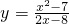 (1<x<
(1<x< );
); ;
;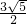 ;AB、AD、BC.
;AB、AD、BC.

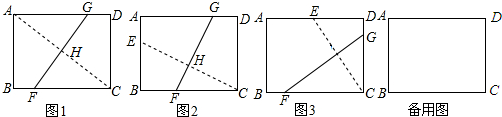
 如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.
如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.