
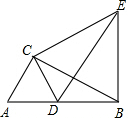
 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为$\sqrt{3}$.
如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为$\sqrt{3}$. 分析 先根据直角三角形的性质求出BC、AB的长,再根据图形旋转的性质得出AC=DC,BC=EC,再由DB=AD即可得出∠DCB=30°,故可得出∠BCE=60°,进而判断出△BCE是等边三角形,故可得出结论.
解答 解:∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,
∴AB=2,BC=$\sqrt{3}$,
∵∠A=60°,将△ABC绕点C逆时针旋转至△CDE,
∴AC=DC,
∴△ADC是等边三角形,
∴AD=$\frac{1}{2}$AB=1,
∴DC=DB,
∴∠DCB=∠DBC=30°,
∵△CDE是△ABC旋转而成,
∴∠DCE=90°,BC=EC,
∴∠ECB=90°-30°=60°,
∴△BCE是等边三角形,
∴BE=BC=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查的是图形旋转的性质及等边三角形的判定定理,熟知旋转前后的图形全等是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某篮球运动员在同一条件下进行“定点投篮”练习,结果如表所示:
某篮球运动员在同一条件下进行“定点投篮”练习,结果如表所示:| 投篮总次数n | 10 | 50 | 100 | 200 | 500 |
| 进球的次数m | 6 | 39 | 80 | 160 | 400 |
| 投篮命中率$\frac{m}{n}$ | 0.6 | 0.78 | 0.8 | 0.8 | 0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均分不变,方差不变 | B. | 平均分变大,方差不变 | ||
| C. | 平均分不变,方差变大 | D. | 平均分变大,方差变大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知直线AB:y=$\frac{2}{3}$x+4交x轴于点A,交y轴于点B.直线CD:y=-$\frac{1}{3}$x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
如图,在平面直角坐标系xOy中,已知直线AB:y=$\frac{2}{3}$x+4交x轴于点A,交y轴于点B.直线CD:y=-$\frac{1}{3}$x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
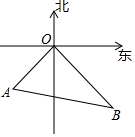 如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.
如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com