
���� ��1�����������֪�������е���ȹ�ϵ�ǡ�A���ͺŷ�װ12����B���ͺŷ�װ8������Ҫ1880Ԫ���͡�A���ͺŷ�װ9����B���ͺŷ�װ10������Ҫ1810Ԫ�����з�������⼴�ɣ�
��2�����蹺��B�ַ�װm������A�ַ�װ��������34-m���г�����ʽ��ɣ�
��3�����װ�깺��B�ַ�װm���г���������ʽ�������ֵ��ɣ�
��� �⣨1����A��װ����ΪxԪ��B��װ����ΪyԪ��������ã�$\left\{\begin{array}{l}{12x+8y=1880}\\{9x+10y=1810}\end{array}\right.$��
��ã�x=90��y=100��
��A��װ����Ϊ90Ԫ��B��װ����Ϊ100Ԫ��
��2�����װ�깺��B�ַ�װm����������ã�
18����34-m��+30m��906
��ã�m$��24\frac{1}{2}$��
�𣺷�װ�깺��B�ַ�װ����25����
��3�����װ�깺��B�ַ�װm�������ַ�װ���ܳɱ�ΪwԪ�� ������ã�
w100m+90��34-m��=10m��
��Ϊw����m��������������Ե�m ȡ��Сֵ��25ʱ��w��СΪ3310��
�𣺷�װ�깺��A��9��B��25����װ������ʹ�����ַ�װ���ܳɱ���ͣ����Ϊ3310Ԫ��
���� ���⿼���˶�Ԫһ�η�����Ͳ���ʽ��Ӧ�ã����ö�Ԫһ�η���������Ӧ����һ�����������Ҫ����2��������ϵ��ȷ���ҵ�������ϵ���÷������ʾ�����ǽ���Ĺؼ������������ò���ʽ��������������ʱ���������ڽⲻ��ʽ�Ľ��������ʵ�������е��������⣬����Щ��������ĸ������ǿ��еķ���������


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
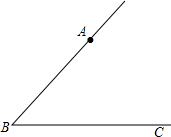 ��ͼ�⣺��AΪ��ABC�ı�AB�ϵ�һ�㣬����A��ֱ��EF��BC���ó߹���ͼ����д������������ͼ�ۼ�����
��ͼ�⣺��AΪ��ABC�ı�AB�ϵ�һ�㣬����A��ֱ��EF��BC���ó߹���ͼ����д������������ͼ�ۼ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.7 | B�� | 0.3 | C�� | 30 | D�� | 70 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com