
【题目】数学李老师给学生出了这样一个问题:探究函数![]() 的图象与性质.小斌根据学习函数的经验,对函数
的图象与性质.小斌根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
(1)函数![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值,请直接写出m的值,m=______;

(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数![]() 的一条性质.
的一条性质.
【答案】(1)自变量x的取值范围是x≠-1;
(2)m=3;
(3)画出函数的图象见解析;
(4)写出函数![]() 的一条性质略,只要符合均给分.
的一条性质略,只要符合均给分.
【解析】(1)根据4分母非零即可得到x+1≠0,解之即可得出x的取值范围;
(2)将y=![]() 代入函数解析式中求出x的值即可;
代入函数解析式中求出x的值即可;
(3)描点、连线画出函数图象;
(4)观察函数图象,写出函数的一条性质即可.
解:(1)∵x+1≠0,
∴x≠-1.
故答案为:x≠-1.
(2)当y=![]() 时,x=3.
时,x=3.
故答案为:3. ![]() 在x<-1和x>-1上均单调递增.
在x<-1和x>-1上均单调递增.
描点、连线画出图象如图所示.
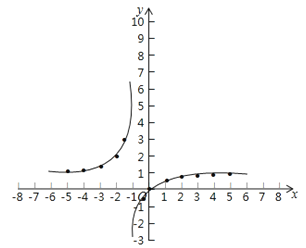
(4)观察函数图象,发现:函数y= ![]() 在x<-1和x>-1上均单调递增.
在x<-1和x>-1上均单调递增.
“点睛”本题考查了反比例函数的性质以及函数图象,根据给定数据描点、连线画出函数图象是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列运算正确的是 ( )
A.(a-2b) (a-2b)=a ![]() -4b
-4b ![]()
B.(P-q) ![]() =P
=P ![]() -q
-q ![]()
C.(a+2b) (a-2b)=-a ![]() -2b
-2b ![]()
D.(-s-t) ![]() =s
=s ![]() +2st+t
+2st+t ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 有两边和一角相等的两个三角形全等 B. 有一角相等的两个等腰三角形全等
C. 有一边相等的两个等腰直角三角形全等 D. 有一边相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
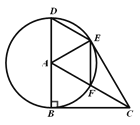
【题目】在Rt△ABC中,∠ABC=90°,以点A为圆心,AB为半径,作⊙A交AC于点F,交BA的延长线于点D,过点D作AC的平行线交⊙A于点E,连接AE、CE,EF.
⑴求证:CE⊥AE;
⑵当∠CAB等于多少度时,四边形ADEF为菱形,并给于证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com