
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| A”¢Ö±½ĒČż½ĒŠĪ | B”¢µČŃüČż½ĒŠĪ | C”¢µČŃüÖ±½ĒČż½ĒŠĪ | D”¢µČ±ßČż½ĒŠĪ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
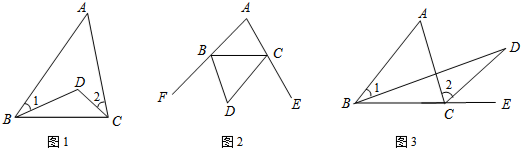
 ČēĶ¼£¬ŅŃÖŖABCÖŠ£¬ADĪŖBC±ßÉĻµÄÖŠĻߣ¬ĒŅAB=4cm£¬AC=3cm£¬ŌņADµÄȔֵ·¶Ī§ŹĒ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖABCÖŠ£¬ADĪŖBC±ßÉĻµÄÖŠĻߣ¬ĒŅAB=4cm£¬AC=3cm£¬ŌņADµÄȔֵ·¶Ī§ŹĒ£Ø””””£©| A”¢3£¼AD£¼4 | ||||
| B”¢1£¼AD£¼7 | ||||
CӢ
| ||||
DӢ
|
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 |
| 2 |
| A”¢Čń½ĒČż½ĒŠĪ |
| B”¢Ö±½ĒČż½ĒŠĪ |
| C”¢¶Ū½ĒČż½ĒŠĪ |
| D”¢µČŃüČż½ĒŠĪ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
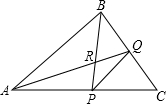 ČēĶ¼£¬ŅŃÖŖ”÷ABC£¬”ĻBµÄĘ½·ÖĻß½»±ßACÓŚP£¬”ĻAµÄĘ½·ÖĻß½»±ßBCÓŚQ£¬Čē¹ū¹żµćP”¢Q”¢CµÄŌ²Ņ²¹ż”÷ABCµÄÄŚŠÄR£¬ĒŅPQ=1£¬ŌņPRµÄ³¤µČÓŚ
ČēĶ¼£¬ŅŃÖŖ”÷ABC£¬”ĻBµÄĘ½·ÖĻß½»±ßACÓŚP£¬”ĻAµÄĘ½·ÖĻß½»±ßBCÓŚQ£¬Čē¹ū¹żµćP”¢Q”¢CµÄŌ²Ņ²¹ż”÷ABCµÄÄŚŠÄR£¬ĒŅPQ=1£¬ŌņPRµÄ³¤µČÓŚ²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com