【题目】教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：25）能喝到不小于70℃的水，则接通电源的时间可以是当天上午的（ ）.
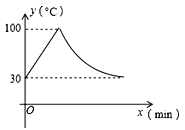
A．7：00 B．7：10 C．7：25 D．7：35
【答案】B.
【解析】
试题首先应用待定系数法求出两个函数的解析式，即y=10x+30（0≤x≤7），
，所以饮水机的一个循环周期为
分钟.当y=70时，10x+30=70，解得x=4，
，解得x=10，即在每个循环周期内，在4≤x≤10时间段内水温不低于70℃.
逐一分析如下：选项A：7:00到8:25之间有85分钟，
，不在4≤x≤10时间段内，故不可行；
选项B：7:10到8:25之间有75分钟，
，在4≤x≤10时间段内，故可行；
选项C：7:25到8:25之间有60分钟，
，不在4≤x≤10时间段内，故不可行；
选项D：7:35到8:25之间有50分钟，
，不在4≤x≤10时间段内，故不可行；
综上所述，只有7:10符合题意.
故选：B.
举一反三期末百分冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】甲、乙两位同学5次数学选拔赛的成绩统计如下表，他们5次考试的总成绩相同，请同学们完成下列问题：
第1 次 | 第2 次 | 第 3次 | 第 4次 | 第5 次 | |
甲成绩 | 90 | 40 | 70 | 40 | 60 |
乙成绩 | 70 | 50 | 70 |
| 70 |
（1）统计表中，求
的值，甲同学成绩的极差为多少；
（2）小颖计算了甲同学的成绩平均数为60，方差是
[(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]＝360.
请你求出乙同学成绩的平均数和方差；
（3）从平均数和方差的角度分析，甲乙两位同学谁的成绩更稳定.
查看答案和解析>>
科目：初中数学 来源： 题型：
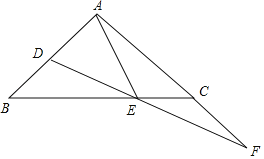
【题目】如图，△ABC中，AB=AC，∠BAC=90°，点D，E分别在AB，BC上，∠EAD=∠EDA，点F为DE的延长线与AC的延长线的交点．
（1）求证：DE=EF；
（2）判断BD和CF的数量关系，并说明理由；
（3）若AB=3，AE=
，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知圆柱体的体积不变，当它的高h＝12.5cm时，底面积S＝20cm2.
(1)求S与h之间的函数解析式；
(2)画出函数图象；
(3)当圆柱体的高为5cm，7cm时，比较底面积S的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
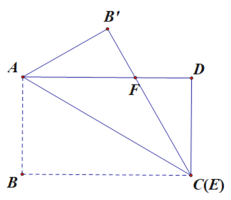
【题目】如图，在矩形纸片ABCD中，已知AB＝2，BC＝
，点E在边CD上移动，连接AE，将多边形ABCE沿直线AE翻折，得到多边形AB′C′E，点B、C的对应点分别为点B′、C′．
（1）当点E与点C重合时，求DF的长；
（2）若B′C′分别交边AD，CD于点F，G，且∠DAE＝22.5°，求△DFG的面积；
（3）如果点M为CD的中点，那么在点E从点C移动到点D的过程中，求C′M的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y1=﹣x+2的图象与反比例函数y2=
的图象交于点A（﹣1，3）、B（n，﹣1）．
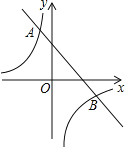
（1）求反比例函数的解析式；
（2）当y1＞y2时，直接写出x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠B=10°，∠ACB=20°，AB=4cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD的中点．
（1）指出旋转中心，并求出旋转的度数；
（2）求出∠BAE的度数和AE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
