
 如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )
如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )| A. | 16 | B. | 15.8 | C. | 15.6 | D. | 15.4 |
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是( )
如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是( )| A. | 4 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米).现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元?
某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米).现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读并填空:
阅读并填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
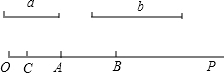 根据所示图形填空:
根据所示图形填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com