
【题目】若抛物线上![]() ,它与
,它与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,
之间的一点,
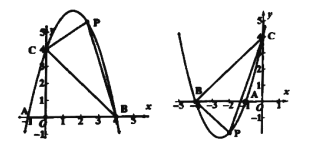
(1)当![]() 时,求抛物线的方程,并求出当
时,求抛物线的方程,并求出当![]() 面积最大时的
面积最大时的![]() 的横坐标。
的横坐标。
(2)当![]() 时,求抛物线的方程及
时,求抛物线的方程及![]() 的坐标,并求当
的坐标,并求当![]() 面积最大时
面积最大时![]() 的横坐标。
的横坐标。
(3)根据(1)、(2)推断![]() 的横坐标与
的横坐标与![]() 的横坐标有何关系?
的横坐标有何关系?
【答案】(1)2;(2)-2;(3)![]() 的横坐标等于
的横坐标等于![]() 的横坐标的一半
的横坐标的一半
【解析】
(1)将k=4代入![]() 化成交点式,然后将C(0,4)代入确定a的值,求得B点坐标,连接OP;设
化成交点式,然后将C(0,4)代入确定a的值,求得B点坐标,连接OP;设![]() ,即可求出△BCP的面积表达式,然后求最值即可.
,即可求出△BCP的面积表达式,然后求最值即可.
(2)设![]() ,将
,将![]() 代入得
代入得![]() ,得到二次函数解析式;令y=0,求出直线BC所在的直线方程;过
,得到二次函数解析式;令y=0,求出直线BC所在的直线方程;过![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于
于![]() ,设
,设![]() 、
、![]() ,求出△BCP的面积表达式,然后求最值即可.
,求出△BCP的面积表达式,然后求最值即可.
(3)由(1)(2)的解答过程,进行推断即可.
解:(1)![]() 时,
时,
由交点式得![]() ,
,
![]() 代入得
代入得![]() ,
,
∴![]() ,
,
∵k=4
∴B点坐标![]() ;
;
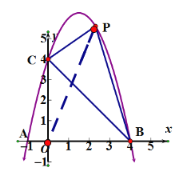
连![]() ,设
,设![]() ,
,
![]()
![]()
![]()
![]() 时,最大值为8,
时,最大值为8,
∴![]() 的横坐标为2时有最大值.
的横坐标为2时有最大值.
(2)当![]() 时,
时,![]() ,
,
设![]() ,
,
![]() 代入得
代入得![]() ,
,
∴![]() .
.
令![]() 求得
求得![]() ,
,
易求直线![]() 方程为
方程为![]() ,
,

过![]() 作
作![]() 平行于
平行于![]() 轴交直线
轴交直线![]() 于
于![]() ,
,
设![]() 、
、![]() ,
,
![]()
![]()
![]()
![]() 面积最大值为8,
面积最大值为8,
此时P的横坐标为-2.
(3)根据(1)(2)得,面积最大时![]() 的横坐标等于
的横坐标等于![]() 的横坐标的一半.
的横坐标的一半.


科目:初中数学 来源: 题型:
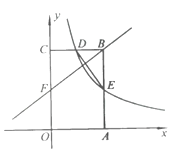
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)直接写出k的值及点E的坐标;
(2)若点F是OC边上一点,且FB⊥DE,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一假期某学校计划组织385名师生租车旅游,现知道出租公司有42座和60座客车,每辆42座比每辆60座客车租金便宜140元,租3辆42座和2每辆60座客车租金共计1880元
(1) 求两种车租金每辆各多少元?
(2) 若学校同时租用这两种客车8辆(可以坐不满),总租金不超过3200元,有几种租车方案?请选择最节省的租车方案
查看答案和解析>>
科目:初中数学 来源: 题型:
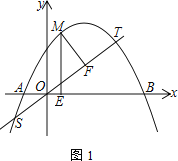
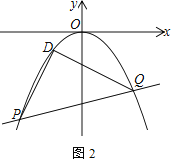
【题目】已知抛物线C:y=ax2-2ax+c经过点C(1,2),与x轴交于A(-1,0)、B两点
(1) 求抛物线C的解析式
(2) 如图1,直线![]() 交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
(3) 如图2,平移抛物线C的顶点到原点得抛物线C1,直线l:y=kx-2k-4交抛物线C1于P、Q两点,在抛物线C1上存在一个定点D,使∠PDQ=90°,求点D的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
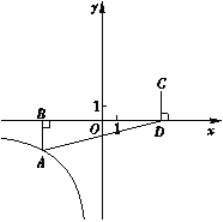
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、丙两地相距500km,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线ABCD表示两车之间的距离y(km)与慢车行驶的时间为x(h)之间的函数关系.根据图中提供的信息,下列说法不正确的是( )
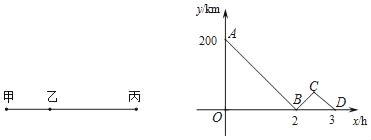
A. 甲、乙两地之间的距离为200 kmB. 快车从甲地驶到丙地共用了2.5 h
C. 快车速度是慢车速度的1.5倍D. 快车到达丙地时,慢车距丙地还有50 km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com