
分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}-(x-1)^{2}}{x-1}$÷$\frac{(2x-1)^{2}}{-(x-1)}$=-$\frac{2x-1}{x-1}$•$\frac{x-1}{(2x-1)^{2}}$=-$\frac{1}{2x-1}$,
当x=sin60°+tan45°═$\frac{\sqrt{3}}{2}$+1时,原式=-$\frac{1}{\sqrt{3}+1}$=-$\frac{1-\sqrt{3}}{2}$.
点评 此题考查了分式的化简求值,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
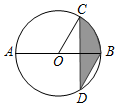 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )| A. | 4π | B. | 2π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com