
【题目】如图,过y轴上一点P(0,1)作平行于x轴的直线PB,分别交函数y1=x2(x≥0)与y2= ![]() (x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016=
(x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016= 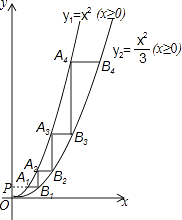
【答案】31511( ![]() ﹣1)
﹣1)
【解析】解:如图, 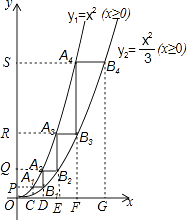
当y=1时,由x2=1 (x≥0),得:x=1,即点A1(1,1),
由 ![]() =1(x≥0),得:x=
=1(x≥0),得:x= ![]() ,即B1(
,即B1( ![]() ,1),
,1),
当x= ![]() 时,y=x2=(
时,y=x2=( ![]() )2=3,即A2(
)2=3,即A2( ![]() ,3),
,3),
∴A1B1= ![]() ﹣1、A2B1=2;
﹣1、A2B1=2;
当y=3时,由 ![]() =3(x≥0),得:x=3,即B2(3,3),
=3(x≥0),得:x=3,即B2(3,3),
当x=3时,y=x2=32=9,即A3(3,9),
∴A2B2=3﹣ ![]() 、A3B2=6;
、A3B2=6;
当y=9时,由 ![]() =9(x≥0),得:x=3
=9(x≥0),得:x=3 ![]() ,即B3(3
,即B3(3 ![]() ,9),
,9),
∴A3B3=3 ![]() ﹣3;
﹣3;
当x=3 ![]() 时,y=x2=(3
时,y=x2=(3 ![]() )2=27,即A4(3
)2=27,即A4(3 ![]() ,27),
,27),
∴A4B3=18;
当y=27是,由 ![]() =27(x≥0),得:x=9,即B4(9,27),
=27(x≥0),得:x=9,即B4(9,27),
∴A4B4=9﹣3 ![]() ;
;
则S1= ![]() ×2×(
×2×( ![]() ﹣1)=
﹣1)= ![]() ﹣1,
﹣1,
S2= ![]() ×2×(3﹣
×2×(3﹣ ![]() )=3﹣
)=3﹣ ![]() =
= ![]() (
( ![]() ﹣1),
﹣1),
S3= ![]() ×6×(3﹣
×6×(3﹣ ![]() )=3(3﹣
)=3(3﹣ ![]() )=3
)=3 ![]() (
( ![]() ﹣1),
﹣1),
S4= ![]() ×6×(3
×6×(3 ![]() ﹣3)=9(
﹣3)=9( ![]() ﹣1),
﹣1),
S5= ![]() ×18×(3
×18×(3 ![]() ﹣3)=27(3
﹣3)=27(3 ![]() ﹣3)=(3
﹣3)=(3 ![]() )2×(
)2×( ![]() ﹣1),
﹣1),
∴S2015= ![]() ×(
×( ![]() ﹣1)=(3
﹣1)=(3 ![]() )1007(
)1007( ![]() ﹣1),
﹣1),
S2016= ![]() S2015=(3
S2015=(3 ![]() )1007(
)1007( ![]() ﹣1)×
﹣1)× ![]() =31511(
=31511( ![]() ﹣1),
﹣1),
所以答案是:31511( ![]() ﹣1).
﹣1).


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AB=BC=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,点D的对应点为D′,连接D′B.若△D′BC为等边三角形,则DE=____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A,B 之间的距离记为|AB|.请回答问题:
(1)直接写出a,b, |AB|的值. a= ,b = , |AB|= ;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(3)若点P在点A的左侧,M、N分别是PA、PB的中点.当点P在点A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( ) 
A.L,K
B.C
C.K
D.L,K,C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P与y轴相切,交直线y=x于A,B两点,已知圆心P的坐标为(2,a)(a>2),AB=2 ![]() ,则a的值为( )
,则a的值为( ) 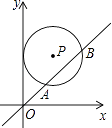
A.4
B.2+ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com